在△ABC中，∠ABC=90°，將△ABC繞點A逆時針旋轉得到△ADE（點B的對應點是點D，且0°＜∠BAD＜180°），射線DE與直線CB交于點M．
（1）如圖1，當∠BAD=90°時，求證：四邊形ADMB是正方形；
（2）如圖2，當點D在線段CA的延長線上時，若AB=1，AC=3，求線段ME的長；
（3）如圖3，過點A作AN∥DE，交線段CB于點N，AN平分∠CAE，試探索：CN與MN的數量關系，并說明理由．
【考點】四邊形綜合題．
【答案】（1）見解析；
（2）ME=；
（3）CN=MN，理由見解析．
（2）ME=
2
（3）CN=MN，理由見解析．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：156引用：1難度：0.6
相似題
-
1．定義：有一組鄰邊相等且對角互補的四邊形稱為“等補四邊形”．
（1）下列選項中一定是“等補四邊形”的是 ；
A．平行四邊形
B．矩形
C．正方形
D．菱形
（2）如圖1，在邊長為a的正方形ABCD中，E為CD邊上一動點（E不與C、D重合），AE交BD于點F，過F作FH⊥AE交BC于點H．
①試判斷四邊形AFHB是否為“等補四邊形”并說明理由；
②如圖2，連接EH，求三角形CEH的周長；
③若四邊形ECHF是“等補四邊形”，求CE的長．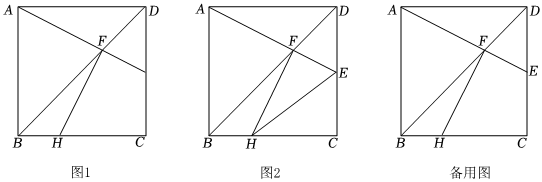
發布：2025/5/22 13:0:1組卷：945引用：5難度：0.2 -
2．（1）如本題圖①，AD為△ABC的角平分線，∠ADC=60°，點E在AB上，AE=AC．求證：DE平分∠ADB．
（2）如本題圖②，在（1）的條件下，F為AB上一點，連結FC交AD于點G．若FB=FC，DG=2，CD=3，求BD的長．
（3）如本題圖③，在四邊形ABCD中，BC=6，CD=5，對角線AC平分∠BAD，∠BCA=2∠DCA，點E為AC上一點，∠EDC=∠ABC．若DE=DC，求AB的長．12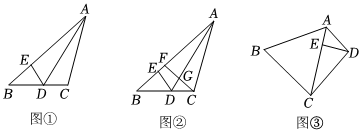
發布：2025/5/22 11:30:2組卷：320引用：1難度：0.3 -
3．我們定義：有一組鄰角相等的凸四邊形叫做“等鄰角四邊形”．
（1）概念理解：
請你根據上述定義舉一個等鄰角四邊形的例子，例如 是等鄰角四邊形；
（2）問題探究：
如圖1，在等鄰角四邊形ABCD中，∠DAB=∠ABC，AD，BC的垂直平分線恰好交于AB邊上一點P，連接AC，BD，試探究AC與BD的數量關系，并說明理由；
（3）應用拓展：
如圖2，在△ABC與△ABD中，∠C=∠D=90°，BC=BD=3，AB=5，將△ABD繞著點A順時針旋轉角α（0°＜∠α＜∠BAC）得到△AB′D′（如圖3），當四邊形AD′BC為等鄰角四邊形時，求出它的面積．
發布：2025/5/22 11:30:2組卷：623引用：2難度：0.2