（1）觀察下列各式的規(guī)律：
（a-b）（a+b）=a²-b²；
（a-b）（a²+ab+b²）=a³-b³；
（a-b）（a³+a²b+ab²+b³）=a⁴-b⁴；
…
可得到（a-b）（a²⁰²⁰+a²⁰¹⁹b+…+ab²⁰¹⁹+b²⁰²⁰）=
a²⁰²¹-b²⁰²¹
a²⁰²¹-b²⁰²¹
．
（2）猜想：（a-b）（a^n-1+a^n-2b+…+ab^n-2+b^n-1）=
aⁿ-bⁿ
aⁿ-bⁿ
（其中n為正整數(shù)，且n≥2）．
（3）利用（2）猜想的結(jié)論計算：2⁹-2⁸+2⁷-…+2³-2²+2．

【答案】a²⁰²¹-b²⁰²¹；aⁿ-bⁿ

【解答】

【點評】

聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。

發(fā)布：2024/8/13 3:0:1組卷：196引用：1難度：0.7

相似題

1．下列各式中，不能用平方差公式計算的是（　　）
A．（-m-1）（-m+1） B．（m-1）（-m-1）
C．（m-1）（1+m） D．（m+1）（-m-1）
發(fā)布：2025/6/2 19:0:1組卷：505引用：5難度：0.7
解析
2．計算：
3
-
64
-（
2
+1）（
2
-1）．
發(fā)布：2025/6/3 0:30:1組卷：34引用：1難度：0.8
解析
3．從圖1到圖2的變化過程可以發(fā)現(xiàn)的結(jié)論是（　　）
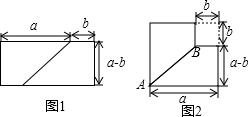
A．（a+b）（a-b）=a²-b² B．（a-b）²=a²-2ab+b²
C．（a+b）²=a²+2ab+b² D．a(chǎn)²+2ab+b²=（a+b）²
發(fā)布：2025/6/2 22:30:1組卷：359引用：3難度：0.8
解析

相關(guān)試卷

A．（-m-1）（-m+1）	B．（m-1）（-m-1）
C．（m-1）（1+m）	D．（m+1）（-m-1）

A．（a+b）（a-b）=a²-b²	B．（a-b）²=a²-2ab+b²
C．（a+b）²=a²+2ab+b²	D．a(chǎn)²+2ab+b²=（a+b）²

1．下列各式中，不能用平方差公式計算的是（ ）