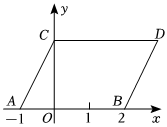
如圖，在平面直角坐標系中，點A、B的坐標分別為（-1，0）、（2，0），現同時將點A、B分別向上平移2個單位，再向右平移1個單位，分別得到點A、B的對應點C、D，連接AC、BD、CD．
（1）若在y軸上存在點M，連接MA、MB，使S△MAB=S平行四邊形ABDC，求出點M的坐標；
（2）若點P在直線BD上運動，連接PC、PO，若P在線段BD之間時（不與B、D重合），求S△CDP+S△BOP的取值范圍；
（3）若點P在第一、四象限，且在直線BD上運動，請直接寫出∠CPO、∠DCP、∠BOP的數量關系．
【考點】四邊形綜合題．
【答案】（1）M（0，4）或（0，-4）；
（2）2＜S△CDP+S△BOP＜3；
（3）∠CPO=∠DCP+∠BOP或∠POB=∠DCP+∠CPO或∠DCP=∠POB+∠CPO．
（2）2＜S△CDP+S△BOP＜3；
（3）∠CPO=∠DCP+∠BOP或∠POB=∠DCP+∠CPO或∠DCP=∠POB+∠CPO．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/20 8:0:8組卷：92引用：1難度：0.1
相似題
-
1．如圖1，四邊形ABCD為正方形，點E為其邊BC上一點，以CE為邊在正方形ABCD右側作正方形CEFG，將正方形CEFG繞點C逆時針旋轉，記旋轉角為α（0°＜α＜360°），連接AF、BG，直線AF、BG交于點M．
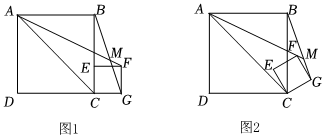
（1）當α=90°時，∠AMB=°；當α=270°時，∠AMB=°；
（2）在旋轉過程中，∠AMB的度數是否為定值？如果是，請就圖2的情況予以證明；如果不是，請說明理由．
（3）若BC=3，CE=1，當A、E、F三點在同一條直線上時，請直接寫出線段BM的長度．發布：2025/5/25 13:0:1組卷：152引用：1難度：0.1 -
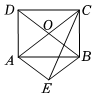2．如圖，矩形ABCD的對角線AC，BD相交于點O，△AOB關于AB的對稱圖形為△AEB．
（1）求證：四邊形AEBO是菱形；
（2）連接CE，若AB=6cm,CB=cm.21
①求sin∠ECB的值；
②若點P為線段CE上一動點（不與點C重合），連接OP，一動點Q從點O出發，以1cm/s的速度沿線段OP勻速運動到點P，再以2.5cm/s的速度沿線段PC勻速運動到點C，到達點C后停止運動，當點Q沿上述路線運動到點C所需要的時間最短時，求PC的長和點Q走完全程所需的時間．發布：2025/5/25 13:30:1組卷：46引用：2難度：0.3 -
3．課本再現
（1）在證明“三角形內角和定理”時，小明只撕下三角形紙片的一個角拼成圖1即可證明，其中與∠A相等的角是 ；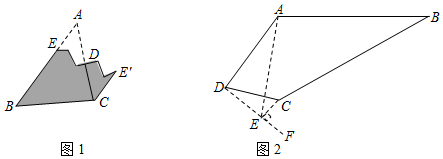
類比遷移
（2）如圖2，在四邊形ABCD中，∠ABC與∠ADC互余，小明發現四邊形ABCD中這對互余的角可類比（1）中思路進行拼合：先作∠CDF=∠ABC，再過點C作CE⊥DF于點E，連接AE，發現AD，DE，AE之間的數量關系是 ；
方法運用
（3）如圖3，在四邊形ABCD中，連接AC，∠BAC=90°，點O是△ACD兩邊垂直平分線的交點，連接OA，∠OAC=∠ABC．
①求證：∠ABC+∠ADC=90°；
②連接BD，如圖4，已知AD=m,DC=n,=2，求BD的長（用含m,n的式子表示）．ABAC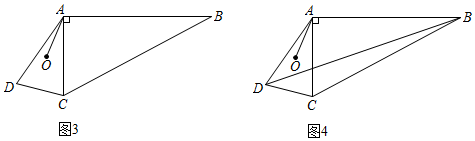
發布：2025/5/25 13:30:1組卷：2913引用：8難度：0.1