（1）如圖1，在矩形ABCD中，AB=4，BC=10，若要在該矩形中作出一個面積最大的△BPC，且使∠BPC=90°，求滿足條件的點P到點A的距離．
（2）如圖2，有一座古井O，按規定，要以井O為對稱中心，建一個面積盡可能大的形狀為平行四邊形的景區ABCD．根據實際情況，要求頂點A是定點，點A到井O的距離為403米，∠BAD=120°，那么，是否可以建一個滿足要求的面積最大的平行四邊形景區ABCD？若可以，求出滿足要求的平行四邊形ABCD的最大面積；若不可以，請說明理由．（井O的占地面積忽略不計）
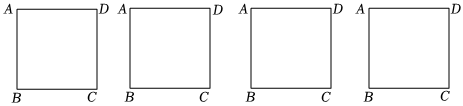
（3）為了保護古井O（井O的占地面積忽略不計），擬以古井O為中心劃定邊長為30米的正方形景區，在該正方形區域內選擇若干個安裝點，安裝一種電訊信號轉發裝置，其發射直徑為31米．現要求：在該正方形區域每個點安裝一個這種轉發裝置，使這些裝置轉發的信號能完全覆蓋這個景區．問：
①能否找到這樣的4個安裝點，使得這些點安裝了這種轉發裝置后能達到預設的要求？
②至少需要選擇多少個安裝點，才能使這些點安裝了這種轉發裝置后達到預設的要求？
答題要求：請你在解答時，畫出必要的示意圖，并用必要的計算、推理和文字來說明你的理由．（下面給出了幾個邊長為30米的正方形區域示意圖，供解題時選用）
40
3
【考點】四邊形綜合題．
【答案】（1）2或8；
（2）可以，最大為平方米；
（3）①能，見解析；
②至少3個安裝點，見解析．
（2）可以，最大為
9600
3
（3）①能，見解析；
②至少3個安裝點，見解析．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：114引用：3難度：0.1
相似題
-
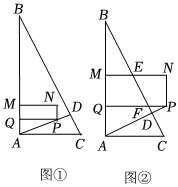1．如圖①，在△ABC中，∠BAC=90°，AC=4，AB=8，AD⊥BC，動點P從點A出發，沿射線AD以每秒個單位長度的速度運動，過點P作AB的垂線交AB于點Q，以PQ為邊向上作矩形PQMN，點M在AB或AB的延長線上，PQ=2QM，當點Q與點B重合時點P停止運動，設點P運動的時間為t（秒）．5
（1）求BC的長；
（2）當BC平分矩形PQMN的周長時，求t的值；
（3）當點N在△ABC的直角邊的垂直平分線上時，直接寫出t的值；
（4）如圖②，當點P在AD的延長線上時，MN、PQ分別交邊BC于點E、F，當△PFD與圖中某個三角形全等時，求t的值．發布：2025/5/23 10:30:1組卷：100引用：1難度：0.2 -
2．如圖1，在平行四邊形ABCD中，AC與BD交于點O，EF∥BD，且EF交AC于點M．
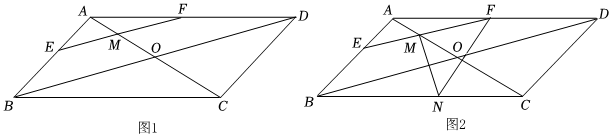
（1）求證：EM=FM；
（2）如圖2，過點M作MN⊥EF交BC于點N，連接NF，若∠BNM=2∠EFN，∠FNC=50°，∠ADC=45°，FN=8．
①求BN的長；
②若，求AE=32．S△AEMS四邊形MODF發布：2025/5/23 11:0:1組卷：117引用：1難度：0.5 -
3．綜合與實踐
在綜合實踐課上，同學們以“正方形的旋轉”為主題開展學習數學活動．
操作判斷
（1）操作一：將正方形ABCD與正方形AEFG的頂點A重合，點G在正方形ABCD的邊AD上，如圖1，連接CF，取CF的中點O，連接DO，OG．操作發現，DO與OG的位置關系是 ；DO與OG的數量關系是 ；
（2）操作二：將正方形AEFG繞頂點A順時針旋轉，（1）中的兩個結論是否仍然成立？如果成立，請僅就圖2的情形進行證明；如果不成立，請說明理由；
拓展應用
（3）若AB=4，AE=2，當∠BAG=150°時，請直接寫出DO的長．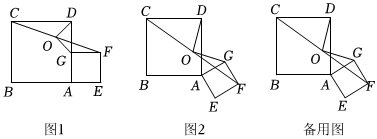
發布：2025/5/23 11:30:2組卷：456引用：6難度：0.3