2022年江蘇省鹽城市鹿鳴路中學中考數學模擬試卷(5月份)
發布:2024/12/5 1:0:2
一、選擇題(本大題共有8小題,每小題3分,共24分。在每小題所給出的四個選項中,只有一項是合題目要求的,請將正確選項的字母代號填涂在答題卡相應位置上)
-
1.2022的倒數是( )
A.2022 B.-2022 C. 12022D.- 12022組卷:1139引用:71難度:0.8 -
2.下列圖形中,是軸對稱圖形的有( )

A.1個 B.2個 C.3個 D.4個 組卷:22引用:2難度:0.8 -
 3.如圖,數軸上點M、N對應的數分別為m、n,則下列不等式正確的是( )
3.如圖,數軸上點M、N對應的數分別為m、n,則下列不等式正確的是( )A.m>n B.m+n<0 C.-2m>-2n D.mn<0 組卷:179引用:2難度:0.6 -
 4.用5個完全相同的小正方體組合成如圖所示的立體圖形,它的俯視圖為( )
4.用5個完全相同的小正方體組合成如圖所示的立體圖形,它的俯視圖為( )A. 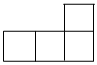
B. 
C. 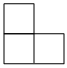
D. 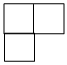 組卷:9引用:1難度:0.7
組卷:9引用:1難度:0.7 -
5.厲害了,我的國!“中國制造”震撼世界.2021年底我國高速公路已開通里程數達14.65萬公里,居世界第一,將數據146500用科學記數法表示正確的是( )
A.1.465×106 B.1.465×105 C.14.65×104 D.1465×103 組卷:11引用:2難度:0.9 -
6.下列運算正確的是( )
A.a3?a4=a12 B.(a3)2=a5 C.(3a2)3=27a6 D.a6÷a3=a2 組卷:1548引用:11難度:0.9 -
7.下列說法正確的是( )
A.要調查現在人們在數字化時代的生活方式,宜采用抽查的方式 B.若甲組數據的方差是 =0.12,乙組數據的方差是S2=0.03,則甲組數據更穩定S2甲C.一組數據3、4、4、8、6、5的中位數是6 D.設y=(x-a1)2+(x-a2)2+…+(x-an)2,則當x是a1、a2、…、an的平均數時,y的值最大. 組卷:24引用:1難度:0.8 -
8.某游樂場一個不等臂蹺蹺板AB長5.6米,支撐柱OH垂直地面,如圖1,當AB的一端A著地時,AB與地面的夾角的正切值為
;如圖2,當AB的另一端B著地時,AB與地面夾角的正弦值為34,則支撐柱OH的長為( )13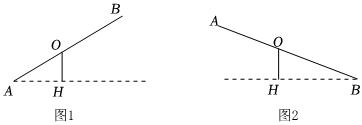
A.0.4 米 B.0.8 米 C. 米3102D.1.2 米 組卷:139引用:4難度:0.5
二、填空題(本大題共有8小題,每小題3分,共24分,不需寫出解答過程,請將答案直接寫在答題卡相應位置上)
-
9.-27的立方根是 .
組卷:2202引用:242難度:0.7
三、解答題(本大題共有11小題,共102分,請在答題卡指定區域內作答,解答時應寫出文字說明、推理過程或演算步驟)
-
26.問題:A4紙給我們矩形的印象,這個矩形是特殊矩形嗎?
思考:通過度量、上網查閱資料,小麗同學發現A4紙的長與寬的比是一個特殊值“”定義:如圖1,點C把線段AB分成兩部分,如果2,那么點C為線段AB的“白銀分割點”如圖2,矩形ABCD中,ACBC=2,那么矩形ABCD叫做白銀矩形.BCAB=2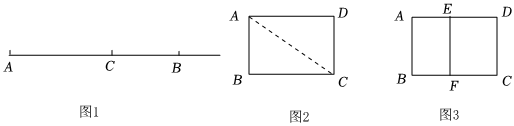
應用:(1)如圖3,矩形ABCD是白銀矩形,AD>AB,將矩形沿著EF對折,求證:矩形ABFE也是白銀矩形.
(2)如圖4,矩形ABCD中,AB=1,BC=,E為CD上一點,將矩形ABCD沿BE折疊,使得點C落在AD邊上的點F處,延長BF交CD的延長線于點G,說明點E為線段GC的”白銀分制點”.2
(3)已知線段AB(如圖5),作線段AB的一個“白銀分割點”.(要求:尺規作圖,保留作圖痕跡,不寫作法) 組卷:299引用:1難度:0.2
組卷:299引用:1難度:0.2 -
27.(1)如圖1,在矩形ABCD中,AB=4,BC=10,若要在該矩形中作出一個面積最大的△BPC,且使∠BPC=90°,求滿足條件的點P到點A的距離.
(2)如圖2,有一座古井O,按規定,要以井O為對稱中心,建一個面積盡可能大的形狀為平行四邊形的景區ABCD.根據實際情況,要求頂點A是定點,點A到井O的距離為米,∠BAD=120°,那么,是否可以建一個滿足要求的面積最大的平行四邊形景區ABCD?若可以,求出滿足要求的平行四邊形ABCD的最大面積;若不可以,請說明理由.(井O的占地面積忽略不計)403
(3)為了保護古井O(井O的占地面積忽略不計),擬以古井O為中心劃定邊長為30米的正方形景區,在該正方形區域內選擇若干個安裝點,安裝一種電訊信號轉發裝置,其發射直徑為31米.現要求:在該正方形區域每個點安裝一個這種轉發裝置,使這些裝置轉發的信號能完全覆蓋這個景區.問:
①能否找到這樣的4個安裝點,使得這些點安裝了這種轉發裝置后能達到預設的要求?
②至少需要選擇多少個安裝點,才能使這些點安裝了這種轉發裝置后達到預設的要求?
答題要求:請你在解答時,畫出必要的示意圖,并用必要的計算、推理和文字來說明你的理由.(下面給出了幾個邊長為30米的正方形區域示意圖,供解題時選用) 組卷:114引用:3難度:0.1
組卷:114引用:3難度:0.1


