閱讀下面的材料：
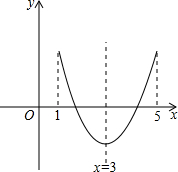
小明在學習中遇到這樣一個問題：若1≤x≤m,求二次函數y=x2-6x+7的最大值．他畫圖研究后發現，x=1和x=5時的函數值相等，于是他認為需要對m進行分類討論．
他的解答過程如下：
∵二次函數y=x2-6x+7的對稱軸為直線x=3，
∴由對稱性可知，x=1和x=5時的函數值相等．
∴若1≤m＜5，則x=1時，y的最大值為2；
若m≥5，則x=m時，y的最大值為m2-6m+7．
請你參考小明的思路，解答下列問題：
（1）當-2≤x≤4時，二次函數y=2x2+4x+1的最大值為4949；
（2）若p≤x≤2，求二次函數y=2x2+4x+1的最大值；
（3）若t≤x≤t+2時，二次函數y=2x2+4x+1的最大值為31，則t的值為1或-51或-5．
【考點】二次函數的最值．
【答案】49；1或-5
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：2394引用：13難度：0.3
