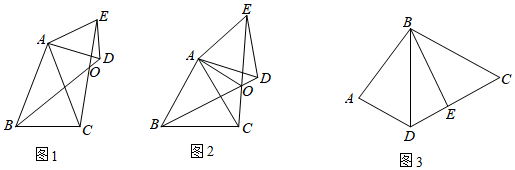
【閱讀材料】小明同學發現這樣一個規律：兩個頂角相等的等腰三角形，如果具有公共的頂角的頂點，并把它們的底角頂點連接起來則形成一組全等的三角形，小明把具有這個規律的圖形稱為“手拉手”圖形．如圖1，在“手拉手”圖形中，小明發現若∠BAC=∠DAE，AB=AC，AD=AE，則△ABD≌△ACE．
【材料理解】（1）在圖1中證明小明的發現．
【深入探究】（2）如圖2，△ABC和△AED是等邊三角形，連接BD，EC交于點O，連接AO，下列結論：①BD=EC；②∠BOC=60°；③∠AOE=60°，其中正確的有 ①②③①②③．（將所有正確的序號填在橫線上）
【延伸應用】（3）如圖3，在四邊形ABCD中，BD=CD，AB=BE，∠ABE=∠BDC=60°，試探究∠A與∠BED的數關系，并證明．
【考點】三角形綜合題．
【答案】①②③
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/27 12:0:2組卷：858引用：8難度：0.4
相似題
-
1．如圖，AB∥CD，點E，F分別在直線AB，CD上，連接EF，EM平分∠AEF交CD于點M，∠MEN=90°，點N在CD上．
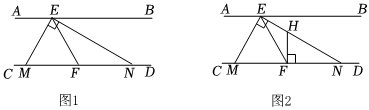
（1）如圖1，若∠AEM=70°，則∠BEN的度數為 ；
（2）求證：點F是MN的中點；
（3）如圖2，過點F作FH⊥CD交EN于點H，猜想線段EM，EH，HN有何數量關系，并說明理由．發布：2025/5/31 12:0:1組卷：38引用：2難度：0.2 -
2．定義：在任意△ABC中，如果一個內角度數的2倍與另一個內角度數的和為90°，那么稱此三角形為“倍角互余三角形．
【基礎鞏固】（1）若△ABC是“倍角互余三角形”，∠C＞90°，∠A=60°，則∠B=°；
【嘗試應用】（2）如圖1，在Rt△ABC中，∠ACB=90°，點D為線段BC上一點，若∠CAD與∠CAB互余．求證：△ABD是“倍角互余三角形”；
【拓展提高】（3）如圖2，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，試問在邊BC上是否存在點E，使得△ABE是“倍角互余三角形”？若存在，請求出BE的長；若不存在，請說明理由．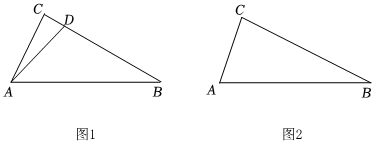
發布：2025/5/31 11:0:1組卷：338引用：1難度：0.1 -
3．對于平面直角坐標系xOy中的點M和圖形G，給出如下定義：點N為圖形G上任意一點，當點P是線段MN的中點時，稱點P是點M和圖形G的“中立點”．
（1）已知點A（4，0），若點P是點A和原點的中立點，則點P的坐標為 ；
（2）已知點B（-2，3），C（1，3），D（-2，0）．
①連接BC，求點D和線段BC的中立點E的橫坐標xE的取值范圍；
②點F為第一、三象限角平分線上的一點，在△BCD的邊上存在點F和△BCD的中立點，直接寫出點F的橫坐標xF的取值范圍．發布：2025/5/31 11:0:1組卷：275引用：1難度：0.4