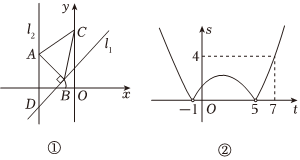
如圖①，在平面直角坐標系中，直線l1：y=x+1與直線l2：x=-2相交于點D，點A是直線l2上的動點，過點A作AB⊥l1于點B，點C的坐標為（0，3），連接AC，BC．設點A的縱坐標為t,△ABC的面積為s.
（1）當t=2時，求點B的坐標；
（2）s關于t的函數解析式為s=14t2+bt-54 （t＜-1或t＞5） a（t+1）（t-5） （-1＜t＜5）
，其圖象如圖②所示，結合圖①、②的信息，求出a與b的值；
（3）在直線l2上是否存在點A，使得∠ACB=90°，若存在，請求出此時點A的坐標；若不存在，請說明理由．
1 4 t 2 + bt - 5 4 | （ t ＜ - 1 或 t ＞ 5 ） |
a （ t + 1 ） （ t - 5 ） | （ - 1 ＜ t ＜ 5 ） |
【考點】一次函數綜合題．
【答案】（1）B（-，）；
（2）a=-；b=-1；
（3）點A的坐標為：（-2，9）或（-2，3）．
1
2
1
2
（2）a=-
1
4
（3）點A的坐標為：（-2，9）或（-2，3）．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/19 8:0:9組卷：62引用：1難度：0.3
相似題
-
1．如圖1，在平面直角坐標系中，直線
分別與x軸、y軸交于點A點和B點，過O點作OD⊥AB于D點，以OD為邊構造等邊△EDF（F點在x軸的正半軸上）．l：y=-33x+43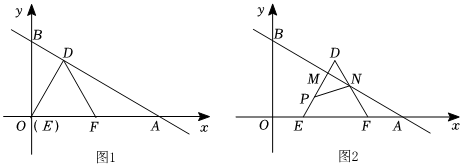
（1）求A、B點的坐標，以及OD的長；
（2）將等邊△EDF，從圖1的位置沿x軸的正方向以每秒1個單位的長度平移，移動的時間為t（s），同時點P從E出發，以每秒2個單位的速度沿著折線ED-DF運動（如圖2所示），當P點到F點停止，△DEF也隨之停止．
①t=（s）時，直線l恰好經過等邊△EDF其中一條邊的中點；
②當點P在線段DE上運動，若DM=2PM，求t的值；
③當點P在線段DF上運動時，若△PMN的面積為，求出t的值．3發布：2025/5/24 3:30:1組卷：471引用：2難度：0.2 -
2．將一個直角三角形紙片ABO，放置在平面直角坐標系中，點A（，0），點B（0，3），點O（0，0）3
（1）過邊OB上的動點D（點D不與點B，O重合）作DE丄OB交AB于點E，沿著DE折疊該紙片，點B落在射線BO上的點F處．
①如圖，當D為OB中點時，求E點的坐標；
②連接AF，當△AEF為直角三角形時，求E點坐標；
（2）P是AB邊上的動點（點P不與點B重合），將△AOP沿OP所在的直線折疊，得到△A′OP，連接BA′，當BA′取得最小值時，求P點坐標（直接寫出結果即可）．發布：2025/5/24 8:0:1組卷：843引用：2難度：0.3 -
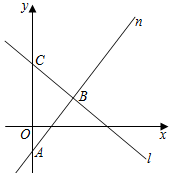3．在如圖的平面直角坐標系中，直線n過點A（0，-2），且與直線l交于點B（3，2），直線l與y軸交于點C．
（1）求直線n的函數表達式；
（2）若△ABC的面積為9，求點C的坐標；
（3）若△ABC是等腰三角形，求直線l的函數表達式．發布：2025/5/24 9:0:1組卷：6355引用：10難度：0.1