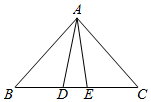
 古希臘數學家歐多克索斯在深入研究比例理論時,提出了分線段的“中末比”問題:點G將一線段MN分為兩線段MG,GN,使得其中較長的一段MG是全長MN與較短的一段GN的比例中項,即滿足MGMN=GNMG=5-12,后人把5-12這個數稱為“黃金分割”數,把點G稱為線段MN的“黃金分割”點.如圖,在△ABC中,已知AB=AC=3,BC=4,若D,E是邊BC的兩個“黃金分割”點,則△ADE的面積為( )
古希臘數學家歐多克索斯在深入研究比例理論時,提出了分線段的“中末比”問題:點G將一線段MN分為兩線段MG,GN,使得其中較長的一段MG是全長MN與較短的一段GN的比例中項,即滿足MGMN=GNMG=5-12,后人把5-12這個數稱為“黃金分割”數,把點G稱為線段MN的“黃金分割”點.如圖,在△ABC中,已知AB=AC=3,BC=4,若D,E是邊BC的兩個“黃金分割”點,則△ADE的面積為( )
MG
MN
GN
MG
5
-
1
2
5
-
1
2
5 | 5 | 5 - 2 5 2 | 5 |
【答案】A
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/5/23 20:19:40組卷:1919引用:24難度:0.6
相似題
-
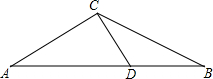 1.如圖,在△ABC中,AC=BC,在邊AB上截取AD=AC,連接CD,若點D恰好是線段AB的一個黃金分割點,則∠A的度數是.發布:2025/5/25 14:0:1組卷:358引用:3難度:0.9
1.如圖,在△ABC中,AC=BC,在邊AB上截取AD=AC,連接CD,若點D恰好是線段AB的一個黃金分割點,則∠A的度數是.發布:2025/5/25 14:0:1組卷:358引用:3難度:0.9 -
2.已知P是線段AB的黃金分割點,且AP<PB,則AP:PB的值是 .
發布:2025/5/25 8:0:2組卷:68引用:2難度:0.6 -
3.寬與長的比是
(約0.618)的矩形叫做黃金矩形,黃金矩形蘊藏著豐富的美學價值,給我們以協調和勻稱的美感.我們可以用這樣的方法畫出黃金矩形:作正方形ABCD,分別取AD、BC的中點E、F,連接EF:以點F為圓心,以FD為半徑畫弧,交BC的延長線于點G;作GH⊥AD,交AD的延長線于點H,則圖中下列矩形是黃金矩形的是( )5-12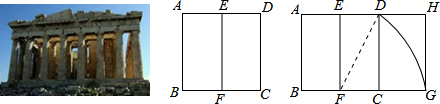
A.矩形ABFE B.矩形EFCD C.矩形EFGH D.矩形DCGH 發布:2025/5/25 10:0:1組卷:5281引用:32難度:0.7


