2023-2024學年湖南省永州市冷水灘區京華中學九年級（上）第一次月考數學試卷

一、單選題（每小題3分，共30分）

• 1．下列各組中的四條線段成比例的是（　　）

  A．3cm、5cm、6cm、9cm	B．3cm、5cm、8cm、9cm
  C．3cm、9cm、10cm、30cm	D．3cm、6cm、7cm、9cm
  組卷：1431引用：15難度：0.5

  解析

• 2．若（-2，y₁）（2，y₂）（3，y₃）在反比例函數

  y

  =

  |

  m

  |

  +

  1

  x

  圖象上，則下列各式正確的是（　　）

  A．y1＜y3＜y2

  B．y3＜y2＜y1

  C．y3＜y1＜y2

  D．y1＜y2＜y3
  組卷：168引用：2難度：0.6

  解析

• 3．已知實數k,現有甲、乙、丙、丁四人對關于x的方程kx²-（k+2）x+

  1

  4

  k=0進行了討論：
  甲說：這一定是關于x的一元二次方程；
  乙說：這有可能是關于x的一元一次方程；
  丙說：當k≥-1時，該方程有實數根；
  丁說：只有當k≥-1且k≠0時，該方程有實數根．
  正確的是（　　）

  A．乙和丙說得對	B．甲和丁說得對
  C．甲和丙說得對	D．乙和丁說得對
  組卷：370引用：9難度：0.7

  解析

• 4．如圖，直線y=ax+b（a≠0）與雙曲線y=

  k

  x

  （k≠0）交于點A（-2，4）和點B（m,-2），則不等式0＜ax+b＜

  k

  x

  的解集是（　　）

  A．-2＜x＜4	B．-2＜x＜0
  C．x＜-2或0＜x＜4	D．-2＜x＜0或x＞4
  組卷：3900引用：16難度：0.5

  解析

• 5．已知一次函數y=mx+n與反比例函數

  y

  =

  m

  x

  ，其中m、n為常數，且mn＜0，則它們在同一坐標系中的圖象可能是（　　）

  A．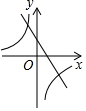

  B．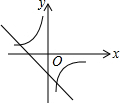

  C．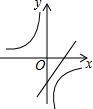

  D．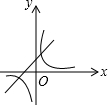
  組卷：933引用：7難度：0.6

  解析

• 6．某公司今年4月的營業額為2500萬元，按計劃第二季度的總營業額要達到9100萬元，設該公司5、6兩月的營業額的月平均增長率為x.根據題意列方程，則下列方程正確的是（　　）

  A．2500（1+x）2=9100

  B．2500（1+x%）2=9100

  C．2500（1+x）+2500（1+x）2=9100

  D．2500+2500（1+x）+2500（1+x）2=9100
  組卷：3064引用：39難度：0.7

  解析

• 7．如圖，已知AB=10，E是AB的中點，且矩形ABCD與矩形ACFE相似，則AC長為（　　）

  A．5

  B．5 2

  C．4 2

  D．6
  組卷：117引用：2難度：0.5

  解析

• 8．將4個數a,b,c,d排成2行，2列，兩邊各加一條豎直線記成

  a	b
  c	d

  ，定義

  a	b
  c	d

  =ad-bc,上述記號就叫做2階行列式．若

  x + 1	x - 1
  2	x + 1

  =7，則x的值為（　　）

  A．±2

  B． ± 10

  C．±4

  D．2
  組卷：61引用：2難度：0.8

  解析

三、解答題（共72分）

• 24．某蔬菜生產基地的氣溫較低時，用裝有恒溫系統的大棚栽培一種新品種蔬菜．如圖是試驗階段的某天恒溫系統從開啟到關閉后，大棚內的溫度y （℃）與時間x（h）之間的函數關系，其中線段AB、BC表示恒溫系統開啟階段，雙曲線的一部分CD表示恒溫系統關閉階段．
  請根據圖中信息解答下列問題：
  （1）求這天的溫度y與時間x（0≤x≤24）的函數關系式；
  （2）求恒溫系統設定的恒定溫度；
  （3）若大棚內的溫度低于10℃時，蔬菜會受到傷害．問這天內，恒溫系統最多可以關閉多少小時，才能使蔬菜避免受到傷害？
  組卷：4273引用：17難度：0.3

  解析

• 25．約定：若關于x的一元二次方程ax²+bx+c=0有兩個實數根分別是x₁，x₂（x₁＜x₂），則稱該方程為“益-Equation”，點（x₁+x₂，x₁?x₂）稱為該方程的“益-Point”，經過該點的直線稱為該方程的一條“益-Line”．
  （1）已知關于x的一元二次方程x²-6x+2m-1=0是“益-Equation”，求m的取值范圍；
  （2）是否存在實數b,c,使得不論k（k≠0）為何值，關于x的“益-Equation”x²+bx+c=0的“益-Point”M始終在直線y=kx-5k+6的圖象上，若存在請求出b,c的值，若不存在，說明理由；
  （3）已知關于x的“益-Equation”x²-（2m+1）x+m²+m=0的兩實根為x₁，x₂（x₁＜x₂），直線y=kx+b是該方程的一條“益-Line”．當x₁≤x≤x₂時，y的取值范圍恰好是2x₁≤y≤2x₂，求直線y=kx+b的解析式．
  組卷：523引用：3難度：0.3

  解析