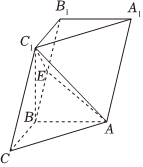
如圖，在三棱柱ABC-A1B1C1中，已知AB⊥側面BB1C1C，BC=2，AB=CC1=2，∠BCC1=π4，點E在棱BB1上．
（1）證明：C1B⊥平面ABC；
（2）若BE=λBB1，試確定λ的值，使得C到平面AC1E的距離為455．
BC
=
2
∠
BC
C
1
=
π
4
4
5
5
【考點】空間中點到平面的距離；直線與平面垂直．
【答案】（1）證明見解析；
（2）或．
（2）
λ
=
1
2
λ
=
3
10
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/6 2:0:8組卷：46引用：4難度：0.6
相似題
-
1．已知A（0，0，2），B（0，2，1），C（2，1，0），D（2，0，1），則點D到平面ABC的距離為（ ）
發布：2024/10/24 16:0:1組卷：175引用：5難度：0.7 -
2．已知正方體ABCD-A1B1C1D1中，AB=2，則點C到平面BDD1B1的距離為（ ）
發布：2024/11/29 18:30:4組卷：215引用：4難度：0.7 -
3．如圖，在三棱錐OABC中，三條側棱OA，OB，OC兩兩垂直，且OA，OB，OC的長分別為a,b,c.M為△ABC內部的任意一點，點M到平面OBC，平面OAC，平面OAB的距離分別為a0，b0，c0，則=（ ）2（a0a+b0b+c0c）發布：2024/10/25 8:0:2組卷：25引用：4難度：0.5