綜合與探究．
問題情境：
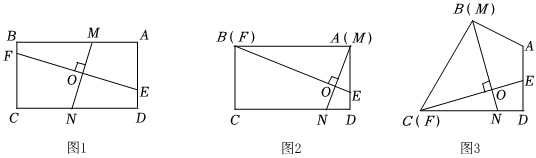
如圖，在矩形ABCD中，點E為邊AD上的動點，點F為邊BC上的動點，點M為邊AB上的動點，連接EF，過點M作MN⊥EF于點O，交邊CD于點N．探究線段FE與MN的比值是否發生變化．
特例探究：
（1）如圖2，當點M與點A重合，點F與點B重合，發現BEAN=ABAD．請證明；
探究發現：
（2）如圖1，探究EFMN=ABAD成立嗎？若成立，請證明；若不成立，請寫出你的發現，并說明理由；
探究拓展：
（3）如圖3，把“矩形ABCD”改為“四邊形ABCD，BC=CD，∠BCD=60°，∠ADC=90°，點F與點C重合，點M與點B重合”，其余條件不變，猜想BNCE的值，并證明．
BE
AN
=
AB
AD
EF
MN
=
AB
AD
BN
CE
【考點】相似形綜合題．
【答案】（1）見解析；
（2）成立；
（3）．
（2）成立；
（3）
3
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/8/11 5:0:1組卷：361引用：1難度：0.4
相似題
-
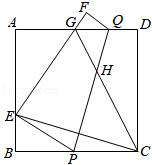1．如圖，將正方形紙片ABCD沿PQ折疊，使點C的對稱點E落在邊AB上，點D的對稱點為點F，EF交AD于點G，連接CG交PQ于點H，連接CE，EH．
（1）求證：△PBE∽△QFG；
（2）求∠ECG的度數；
（3）求證：EG2-CH2=GQ?GD．發布：2025/5/25 21:0:1組卷：400引用：2難度：0.3 -
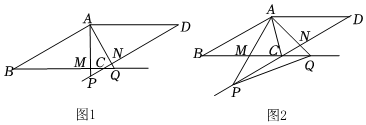2．如圖1，在菱形ABCD中，∠ABC是銳角，P、Q分別是邊DC、BC延長線上的動點，連接AP、AQ分別交BC、DC于點M、N．
（1）當AP⊥BC且∠PAQ=∠D時，證明：△ABM≌△ADN；
（2）如圖2，當∠PAQ=∠BCD時，連接AC、PQ．12
①證明：AC2=CP?CQ；
②若AB=4，AC=2，則當CM為何值時，△APQ是以PQ為底邊的等腰三角形．發布：2025/5/25 21:30:1組卷：184引用：1難度：0.1 -
3．【證明體驗】（1）如圖1，△ABC中，D為BC邊上任意一點，作DE⊥AC于E，若∠CDE=
∠A，求證：△ABC為等腰三角形；12
【嘗試應用】
（2）如圖2，四邊形ABCD中，∠D=90°，AD=CD，AE平分∠BAD，∠BCD+∠EAD=180°，若DE=2，AB=6，求AE的長；
【拓展延伸】
（3）如圖3，△ABC中，點D在AB邊上滿足CD=BD，∠ACB=90°+∠B，若AC=1012，BC=20，求AD的長．3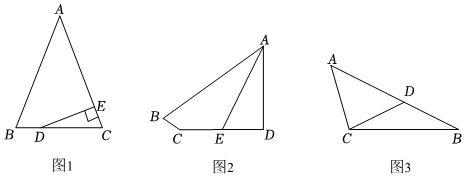
發布：2025/5/25 20:0:1組卷：497引用：1難度：0.3