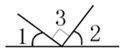
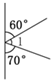
有公共頂點的兩個角，∠AOB=∠COD，且OE為∠BOC的角平分線。

（1）如圖1，請探索∠AOE和∠DOE的大小關系，并說明理由；
（2）如圖2，∠AOE和∠DOE是否仍然滿足（1）中關系？請說明理由；
（3）若∠AOB=90°，∠AOC=64°，求出∠BOE的度數。

【考點】線段與角的綜合．

【答案】（1）∠AOE=∠DOE
DOE
因為OE為∠BOC的角平分線，所以∠BOE=∠COE。而∠AOB=∠COD，所以∠AOB+∠BOE=∠COD+∠COE，即∠AOE=∠DOE。
（2）滿足。
因為OE為∠BOC的角平分線，所以∠BOE=∠COE。而∠AOB=∠COD，所以∠AOB-∠BOE=∠COD-∠COE，即∠AOE=∠DOE。
（3）13°或77°。