我們不妨約定:二次函數(shù)y=ax2+bx+c(a≠0)與x軸交于A、B兩點(diǎn),其中C為頂點(diǎn),當(dāng)△ABC為等腰直角三角形時(shí),我們稱二次函數(shù)為“等腰直角函數(shù)”.
(1)證明y=12x2-3x+52為“等腰直角函數(shù)”;
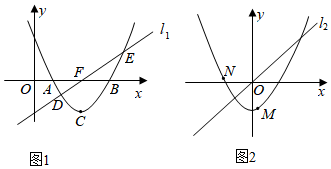
(2)如圖1,在(1)的“等腰直角函數(shù)”圖象中,過AB中點(diǎn)F的直線l1與二次函數(shù)相交于D,E兩點(diǎn),求△CDE面積的最小值;
(3)如圖2,M、N為“等腰直角函數(shù)”y=12x2-2上不重合的兩個(gè)動(dòng)點(diǎn),且關(guān)于過原點(diǎn)的直線l2對(duì)稱,當(dāng)點(diǎn)M的橫坐標(biāo)為1時(shí),求出點(diǎn)N的坐標(biāo).
1
2
x
2
-
3
x
+
5
2
1
2
x
2
【考點(diǎn)】二次函數(shù)綜合題.
【答案】(1)證明過程見解答過程;
(2)4;
(3)N(,-)或N或N.
(2)4;
(3)N(
3
1
2
(
-
3
,-
1
2
)
(
-
1
,-
3
2
)
【解答】
【點(diǎn)評(píng)】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2025/5/21 17:30:1組卷:550引用:2難度:0.3
相似題
-
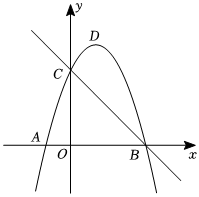 1.如圖所示,拋物線y=-x2+2x+3的圖象與x軸交于A,B兩點(diǎn),與y軸交于點(diǎn)C,連結(jié)BC.
1.如圖所示,拋物線y=-x2+2x+3的圖象與x軸交于A,B兩點(diǎn),與y軸交于點(diǎn)C,連結(jié)BC.
(1)求拋物線頂點(diǎn)D的坐標(biāo);
(2)在直線BC上方的拋物線上有一點(diǎn)M,使得四邊形ABMC的面積最大,求點(diǎn)M的坐標(biāo)及四邊形ABMC面積的最大值;
(3)點(diǎn)E在拋物線上,當(dāng)∠EBC=∠ACO時(shí),直接寫出點(diǎn)E的坐標(biāo).發(fā)布:2025/5/22 1:30:1組卷:160引用:4難度:0.4 -
2.已知點(diǎn)P是二次函數(shù)
圖象的頂點(diǎn).y1=-(x-m+1)2+m2-m-1
(1)小明發(fā)現(xiàn),對(duì)m取不同的值時(shí),點(diǎn)P的位置也不同,但是這些點(diǎn)都在某一個(gè)函數(shù)的圖象上,請(qǐng)協(xié)助小明完成對(duì)這個(gè)函數(shù)表達(dá)式的探究:
①將下表填寫完整:
②描出表格中的五個(gè)點(diǎn),猜想這些點(diǎn)在哪個(gè)函數(shù)的圖象上?求出這個(gè)圖象對(duì)應(yīng)的函數(shù)表達(dá)式,并加以驗(yàn)證;m -1 0 1 2 3 P點(diǎn)坐標(biāo) (-2,1) (-1,-1)
(2)若過點(diǎn)(0,2),且平行于x軸的直線與的圖象有兩個(gè)交點(diǎn)A和B,與②中得到的函數(shù)圖象有兩個(gè)交點(diǎn)C和D,當(dāng)AB=CD時(shí),請(qǐng)求出此時(shí)的m值,寫出求解過程;y1=-(x-m+1)2+m2-m-1
(3)若,E(-1,-54),函數(shù)F(3,-54)的圖象與線段EF只有一個(gè)公共點(diǎn),請(qǐng)結(jié)合函數(shù)圖象,直接寫出m的取值范圍.y1=-(x-m+1)2+m2-m-1發(fā)布:2025/5/22 1:30:1組卷:117引用:3難度:0.2 -
3.已知拋物線y=ax2+bx-4與x軸負(fù)半軸交于點(diǎn)A,與x軸正半軸交于點(diǎn)B,與y軸交于點(diǎn)C,且OB=OC=2OA.直線y=kx-2(k>0)與拋物線交于D,E兩點(diǎn)(點(diǎn)D在點(diǎn)E的左側(cè)),連接OD,OE.
(1)求拋物線的解析式;
(2)若△ODE的面積為,求k的值;42
(3)求證:不論k取何值,拋物線上都存在定點(diǎn)F,使得△DEF是以DE為斜邊的直角三角形.發(fā)布:2025/5/22 2:0:8組卷:643引用:1難度:0.3
相關(guān)試卷


