配方法是數學中重要的思想方法之一，它是指將一個式子的某一部分通過恒等變形化為一個完全平方式或幾個完全平方式的和的方法，這種方法常被用到代數式的變形中，并結合非負數的意義來解決一些問題．我們定義：一個整數能表示成a2+b2（a、b是正整數）的形式，則稱這個數為“完美數”，例如，5是“完美數”．理由：因為5=22+12，所以5是“完美數”．
【解決問題】
（1）已知29是“完美數”，請將它寫成a2+b2（a,b是正整數）的形式 52+2252+22；
（2）若x2-6x+13可配方成（x-m）2+n2（m、n為正整數），則mn=1212；
【探究問題】
（3）已知S=x2+4y2+4x-12y+k（x、y是整數，k是常數），要使S為“完美數”，試求出符合條件的一個k值，并說明理由．
【考點】配方法的應用．
【答案】52+22；12
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：271引用：1難度：0.6
相似題
-
1．（1）已知3m=6，3n=2，求32m+n-1的值；
（2）已知a2+b2+2a-4b+5=0，求（a-b）-3的值．發布：2025/6/7 10:30:1組卷：194引用：3難度：0.5 -
2．閱讀下列材料：
利用完全平方公式，將多項式x2+bx+c變形為（x+m）2+n的形式，然后由（x+m）2≥0就可求出多項式x2+bx+c的最小值．
例題：求x2-12x+37的最小值：
解：x2-12x+37=x2-2x?6+62-62+37=（x-6）2+1
因為不論x取何值，（x-6）2總是非負數，即（x-6）2≥0．
所以（x-6）2+1≥1．
所以當x=6時，x2-12x+37有最小值，最小值是1．
根據上述材料，解答下列問題：
（1）填空：x2-8x+=（x-）2；
（2）將x2+10x-2變形為（x+m）2+n的形式，并求出x2+10x-2的最小值；
（3）如圖所示的第一個長方形邊長分別是2a+5、3a+2，面積為S1；如圖所示的第二個長方形邊長分別是5a、a+5，面積為S2；試比較S1與S2的大小，并說明理由．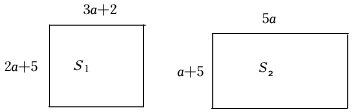
發布：2025/6/7 8:30:2組卷：174引用：1難度：0.4 -
3．在學了乘法公式“（a±b）2=a2±2ab+b2”的應用后，王老師提出問題：求代數式x2+4x+5的最小值．要求同學們運用所學知識進行解答．
同學們經過探索、交流和討論，最后總結出如下解答方法；
解：x2+4x+5=x2+4x+22-22+5=（x+2）2+1，
∵（x+2）2≥0，∴（x+2）2+1≥1．
當（x+2）2=0時，（x+2）2+1的值最小，最小值是1．
∴x2+4x+5的最小值是1．
請你根據上述方法，解答下列各題：
（1）直接寫出（x-1）2+3的最小值為 ．
（2）求代數式x2+10x+32的最小值．
（3）你認為代數式-+2x+5有最大值還是有最小值？求出該最大值或最小值．13x2
（4）若7x-x2+y-11=0，求x+y的最小值．發布：2025/6/7 11:0:1組卷：1135引用：4難度：0.5