某數學興趣小組對線段上的動點問題進行探究，已知AB=8．
問題思考：
如圖1，點P為線段AB上的一個動點，分別以AP、BP為邊在同側作正方形APDC、BPEF．
（1）分別連接AD、DF、AF，AF交DP于點K，當點P運動時，在△APK、△ADK、△DFK中，是否存在兩個面積始終相等的三角形？請說明理由．
問題拓展：
（2）如圖2，若點M、N是線段AB上的兩點，且AM=BN=1，點G、H分別是邊CD、EF的中點，請直接寫出點P從M到N的運動過程中，GH的中點O所經過的路徑的長及OM+ON的最小值．
【考點】三角形綜合題．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：487引用：1難度：0.1
相似題
-
1．閱讀材料，解決問題．
相傳古希臘畢達哥拉斯學派的數學家經常在沙灘上研究數學問題．他們在沙灘上畫點或用小石子來表示數，比如，他們研究過1、3、6、10…，由于這些數可以用圖中所示的三角點陣表示，他們就將每個三角點陣中所有的點數和稱為三角數．
則第n個三角數可以用1+2+3+…+（n-2）+（n-1）+n=（n≥1且為整數）來表示．n（n+1）2
（1）若三角數是55，則n=；
（2）把第n個三角點陣中各行的點數依次換為2，4，6，…，2n,…，請用含n的式子表示前n行所有點數的和；
（3）在（2）中的三角點陣中前n行的點數的和能為120嗎？如果能，求出n,如果不能，請說明理由．發布：2025/5/22 2:0:8組卷：122引用：4難度：0.4 -
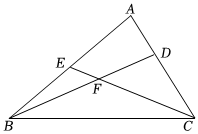2．在△ABC中，BD⊥AC，E為AB邊中點，連接CE，BD與CE相交于點F，過E作EM⊥EF，交BD于點M，連接CM．
（1）依題意補全圖形；
（2）求證：∠EMF=∠ACF；
（3）判斷BM、CM、AC的數量關系，并證明．發布：2025/5/22 6:0:1組卷：1096引用：3難度：0.2 -
3．【初步感知】（1）如圖1，點A，B，C，D均在小正方形網格的格點上，則
=；tan∠BAC2
【問題解決】（2）求tan15°的值；
方案①：如圖2，在△ABC中，∠C=90°，∠BAC=30°，作AD平分∠BAC交BC于D；…
方案②：如圖3，在△ABC中，AB=AC，∠A=30°，過點B作BD⊥AC，垂足為D；…
請你選擇其中一種方案求出tan15°的值（結果保留根號）；
【思維提升】（3）求sin18°的值；如圖4，在△ABC中，AB=AC，∠A=36°．求sin18°的值（結果保留根號）．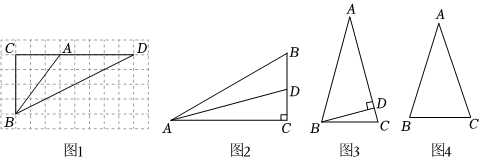
發布：2025/5/21 20:30:1組卷：350引用：4難度：0.1