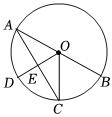
已知Rt△ABC中,∠ACB=90°,CA=CB,有一個圓心角為45°,半徑的長等于CA的扇形CEF繞點C旋轉,且直線CE,CF分別與直線AB交于點M,N.
(Ⅰ)當扇形CEF繞點C在∠ACB的內部旋轉時,如圖1,求證:MN2=AM2+BN2;
(思路點撥:考慮MN2=AM2+BN2符合勾股定理的形式,需轉化為在直角三角形中解決.可將△ACM沿直線CE對折,得△DCM,連DN,只需證DN=BN,∠MDN=90°就可以了.請你完成證明過程.)
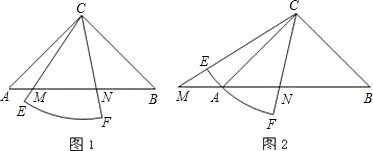
(Ⅱ)當扇形CEF繞點C旋轉至圖2的位置時,關系式MN2=AM2+BN2是否仍然成立?若成立,請證明;若不成立,請說明理由.
【考點】圓心角、弧、弦的關系;勾股定理.
【答案】見試題解答內容
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/27 10:35:59組卷:3305引用:26難度:0.1