2010-2011學年安徽省安慶市潛山縣青樓初中九年級（上）數學競賽試卷

一、選擇題（6小題，每小題4分，共24分）

• 1．a是有理數，則

  11

  a

  +

  2000

  的值不能是（　　）

  A．1

  B．-1

  C．0

  D．-2000
  組卷：225引用：5難度：0.9

  解析

• 2．已知

  a

  =

  -

  1999

  ×

  1999

  -

  1999

  1998

  ×

  1998

  +

  1998

  ，

  b

  =

  -

  2000

  ×

  2000

  -

  2000

  1999

  ×

  1999

  +

  1999

  ，

  c

  =

  -

  2001

  ×

  2001

  -

  2001

  2000

  ×

  2000

  +

  2000

  ，則abc=（　　）

  A．-1

  B．3

  C．-3

  D．1
  組卷：293引用：5難度：0.9

  解析

• 3．如圖，長方形ABCD中，E是AB的中點，F是BC上的一點，且CF=

  1

  3

  BC，則長方形ABCD的面積是陰影部分面積的（　　）倍．

  A．2

  B．3

  C．4

  D．5
  組卷：530引用：7難度：0.9

  解析

• 4．比較2，

  5

  ，

  3

  7

  的大小，正確的是（　　）

  A． 2 ＜ 5 ＜ 3 7

  B． 2 ＜ 3 7 ＜ 5

  C． 3 7 ＜ 2 ＜ 5

  D． 5 ＜ 3 7 ＜ 2
  組卷：638引用：37難度：0.9

  解析

• 5．在平面直角坐標系中，已知線段AB的兩個端點分別是A（-4，-1），B（1，1），將線段AB平移后得到線段A′B′，若點A′的坐標為（-2，2），則點B′的坐標為（　　）

  A．（4，3）

  B．（3，4）

  C．（-1，-2）

  D．（-2，-1）
  組卷：731引用：63難度：0.9

  解析

• 6．如圖，已知AB∥CD∥EF，那么下列結論正確的是（　　）

  A． AD DF = BC CE

  B． BC CE = DF AD

  C． CD EF = BC BE

  D． CE EF = AD AF
  組卷：1157引用：67難度：0.9

  解析

二、填空題．（8小題，每小題4分，共32分）

• 7．如圖，在長方形ABCD中，E是AD的中點，F是CE的中點，若△BDF的面積為6平方厘米，則長方形ABCD的面積是

   

  平方厘米．
  組卷：1151引用：12難度：0.5

  解析

五、應用題．（34分）

• 22．如圖1，拋物線y=ax²-3ax+b經過A（-1，0），C（3，2）兩點，與y軸交于點D，與x軸交于另一點B．
  （1）求此拋物線的解析式；
  （2）若直線y=kx-1（k≠0）將四邊形ABCD面積二等分，求k的值；
  （3）如圖2，過點E（1，-1）作EF⊥x軸于點F，將△AEF繞平面內某點旋轉180°后得△MNQ（點M，N，Q分別與點A，E，F對應），使點M，N在拋物線上，求點M，N的坐標．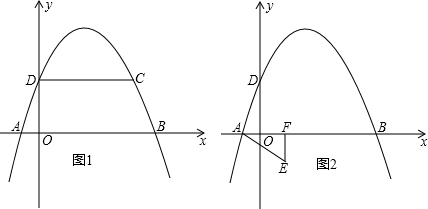
  
  組卷：442引用：17難度：0.1

  解析

• 23．已知Rt△ABC中，∠ACB=90°，CA=CB，有一個圓心角為45°，半徑的長等于CA的扇形CEF繞點C旋轉，且直線CE，CF分別與直線AB交于點M，N．
  （Ⅰ）當扇形CEF繞點C在∠ACB的內部旋轉時，如圖1，求證：MN²=AM²+BN²；
  （思路點撥：考慮MN²=AM²+BN²符合勾股定理的形式，需轉化為在直角三角形中解決．可將△ACM沿直線CE對折，得△DCM，連DN，只需證DN=BN，∠MDN=90°就可以了．請你完成證明過程．）
  （Ⅱ）當扇形CEF繞點C旋轉至圖2的位置時，關系式MN²=AM²+BN²是否仍然成立？若成立，請證明；若不成立，請說明理由．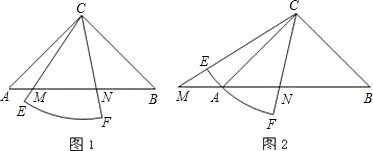
  
  組卷：3304引用：26難度：0.1

  解析