已知點(diǎn)A(0,2),B(0,12),點(diǎn)P為曲線Γ上任意一點(diǎn)且滿足|PA|=2|PB|.
(1)求曲線Γ的方程;
(2)設(shè)曲線Γ與y軸交于M、N兩點(diǎn),點(diǎn)R是曲線Γ上異于M、N的任意一點(diǎn),直線MR、NR分別交直線l:y=3于點(diǎn)F、G.求證:以FG為直徑的圓C與y軸交于定點(diǎn)S,并求出點(diǎn)S的坐標(biāo).
1
2
【考點(diǎn)】曲線與方程.
【答案】(1)x2+y2=1.
(2)當(dāng)x=0時(shí),由x2+y2=1得y=±1,即M(0,1),N(0,-1),
設(shè)點(diǎn)R(x0,y0),(x0≠0),∵點(diǎn)R在曲線Γ上,∴+=1,
直線RM的方程y-1=x,
∴直線RM與直線y=3的交點(diǎn)為F(,3),
直線RN的方程為y+1=x,
∴直線RN與直線y=3的交點(diǎn)為G(,3),
假設(shè)存在點(diǎn)S(0,m),使得以FG為直徑的圓C與y軸交于定點(diǎn)S,
即?=0成立,
則=(,3-m),=(,3-m),
則?=(,3-m)?(,3-m)=0,
即?+(3-m)2=0
即+(3-m)2=0,
∵+=1,
∴-1=-,
即-8+(3-m)2=0得(m-3)2=8,
得m-3==±2,
解得m=3±2,
∴S點(diǎn)的坐標(biāo)為(0,3±2).
(2)當(dāng)x=0時(shí),由x2+y2=1得y=±1,即M(0,1),N(0,-1),
設(shè)點(diǎn)R(x0,y0),(x0≠0),∵點(diǎn)R在曲線Γ上,∴
x
2
0
y
2
0
直線RM的方程y-1=
y
0
-
1
x
0
∴直線RM與直線y=3的交點(diǎn)為F(
2
x
0
y
0
-
1
直線RN的方程為y+1=
y
0
+
1
x
0
∴直線RN與直線y=3的交點(diǎn)為G(
4
x
0
y
0
+
1
假設(shè)存在點(diǎn)S(0,m),使得以FG為直徑的圓C與y軸交于定點(diǎn)S,
即
SF
SG
則
SF
2
x
0
y
0
-
1
SG
4
x
0
y
0
+
1
則
SF
SG
2
x
0
y
0
-
1
4
x
0
y
0
+
1
即
2
x
0
y
0
-
1
4
x
0
y
0
+
1
即
8
x
2
0
y
2
0
-
1
∵
x
2
0
y
2
0
∴
y
2
0
x
2
0
即-8+(3-m)2=0得(m-3)2=8,
得m-3=
±
8
2
解得m=3±2
2
∴S點(diǎn)的坐標(biāo)為(0,3±2
2
【解答】
【點(diǎn)評(píng)】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/10/25 4:0:2組卷:505引用:2難度:0.5
相似題
-
1.關(guān)于曲線C:(x-m)2+(y-m)2=(m-1)2,下列說法正確的是( )
A.曲線C可能經(jīng)過點(diǎn)(0,2) B.若m>1,過原點(diǎn)與曲線C相切的直線有兩條 C.若m=1,曲線C表示兩條直線 D.若m=2,則直線y=x被曲線C截得弦長(zhǎng)等于 22發(fā)布:2024/12/13 4:0:1組卷:62引用:3難度:0.6 -
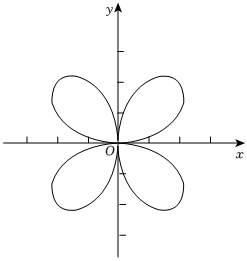 2.四葉草曲線是數(shù)學(xué)中的一種曲線,因形似花瓣,又被稱為四葉玫瑰線(如右圖),其方程為(x2+y2)3=8x2y2,玫瑰線在幾何學(xué)、數(shù)學(xué)、物理學(xué)等領(lǐng)域中有廣泛應(yīng)用.例如,它可以用于制作精美的圖案、繪制圖像、描述物體運(yùn)動(dòng)的軌跡等等.根據(jù)方程和圖象,給出如下4條性質(zhì),其中錯(cuò)誤的是( )
2.四葉草曲線是數(shù)學(xué)中的一種曲線,因形似花瓣,又被稱為四葉玫瑰線(如右圖),其方程為(x2+y2)3=8x2y2,玫瑰線在幾何學(xué)、數(shù)學(xué)、物理學(xué)等領(lǐng)域中有廣泛應(yīng)用.例如,它可以用于制作精美的圖案、繪制圖像、描述物體運(yùn)動(dòng)的軌跡等等.根據(jù)方程和圖象,給出如下4條性質(zhì),其中錯(cuò)誤的是( )A.四葉草曲線方程是偶函數(shù),也是奇函數(shù) B.曲線上兩點(diǎn)之間的最大距離為 22C.曲線經(jīng)過5個(gè)整點(diǎn)(橫、縱坐標(biāo)都是整數(shù)的點(diǎn)) D.四個(gè)葉片圍成的區(qū)域面積小于2π 發(fā)布:2024/12/5 8:30:6組卷:103引用:3難度:0.5 -
 3.中國(guó)傳統(tǒng)文化中很多內(nèi)容體現(xiàn)了數(shù)學(xué)中的“對(duì)稱美”,太極圖是由黑白兩個(gè)魚形紋組成的圓形圖案,充分體現(xiàn)了相互轉(zhuǎn)化、對(duì)稱統(tǒng)一的形式美、和諧美.定義圖象能夠?qū)AO(O為坐標(biāo)原點(diǎn))的周長(zhǎng)和面積同時(shí)等分成兩部分的函數(shù)稱為圓O的一個(gè)“太極函數(shù)”,給出下列命題:
3.中國(guó)傳統(tǒng)文化中很多內(nèi)容體現(xiàn)了數(shù)學(xué)中的“對(duì)稱美”,太極圖是由黑白兩個(gè)魚形紋組成的圓形圖案,充分體現(xiàn)了相互轉(zhuǎn)化、對(duì)稱統(tǒng)一的形式美、和諧美.定義圖象能夠?qū)AO(O為坐標(biāo)原點(diǎn))的周長(zhǎng)和面積同時(shí)等分成兩部分的函數(shù)稱為圓O的一個(gè)“太極函數(shù)”,給出下列命題:
①對(duì)于任意一個(gè)圓O,其“太極函數(shù)”有無(wú)數(shù)個(gè);
②函數(shù)可以是某個(gè)圓O的“太極函數(shù)”;f(x)=ln(x2+1-x)
③函數(shù)可以同時(shí)是無(wú)數(shù)個(gè)圓O的“太極函數(shù)”;f(x)=x23
④函數(shù)y=f(x)是“太極函數(shù)”的充要條件為y=f(x)的圖象是中心對(duì)稱圖形.
其中正確結(jié)論的序號(hào)是( )A.①② B.①②④ C.①③ D.①④ 發(fā)布:2024/12/17 11:30:2組卷:74引用:2難度:0.6


