一數學興趣小組為了測量校園內燈柱AB的高度，設計了以下三個方案：
方案一：在操場上點C處放一面平面鏡，從點C處后退1m到點D處，恰好在平面鏡中看到燈柱的頂部A點的像；再將平面鏡向后移動4m（即FC=4m）放在F處．從點F處向后退1.5m到點H處，恰好再次在平面鏡中看到燈柱的頂部A點的像，測得的眼睛距地面的高度ED、GH為1.5m、已知點B，C，D，F，H在同一水平線上，且GH⊥FH，ED⊥CD，AB⊥BH．（平面鏡的大小忽略不計）
方案二：利用標桿CD測量燈柱的高度．已知標桿CD高1.5m,測得DE=2m,CE=2.5m.
方案三：利用三角板的邊CE保持水平，并且邊CE與點M在同一直線上．已知兩條邊CE=0.4m,EF=0.2m,測得邊CE離地面距離DC=1.5m.
三種方案中，方案 二、三二、三不可行，請選擇可行的方案求出燈柱的高度．
【答案】二、三
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/8/1 8:0:9組卷：95引用：1難度：0.5
相似題
-
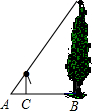1．如圖，小明想測量院子里一棵樹的高度，在某一時刻，他站在該樹的影子上，前后移動，直到他本身的影子的頂端正好與樹影的頂端重疊．此時，他與該樹的水平距離2m,小明身高1.5m,他的影長是1.2m,那么該樹的高度為．發布：2025/6/8 6:30:2組卷：814引用：9難度：0.7 -
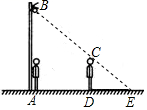2．如圖，小明從路燈下A處，向前走了5米到達D處，在D處發現自己在地面上的影子長DE是2米，如果小明的身高為1.7米，那么路燈離地面的高度AB是 米．發布：2025/6/7 20:0:2組卷：24引用：3難度：0.7 -
3．相同的時間和地點，小明身高1.5米，影長1.2米；樹高多少米，影長2.8米？
發布：2025/6/7 21:30:1組卷：11引用：2難度：0.6