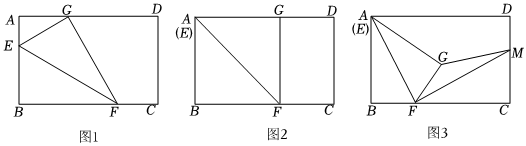
如圖，長方形紙片ABCD，AB=3，BC=5．點E是AB邊上一點，將△BEF沿EF翻折得到△GEF．
【問題解決】（1）如圖1，點B落在邊AD上的點G處，若AE=1，求AG和FG的長；
【類比探究】（2）如圖2，當點E和點A重合時，點B落在邊AD上的點G處，折痕為AF．判定四邊形ABFG的形狀，并說明理由；
【拓展應用】（3）如圖3，當點E和點A重合時，點B落在長方形ABCD內部的點G處，折痕為AF，FM平分∠CFG交CD于點M，連接GM，當GM的長度最短時，求GM的長．
【考點】四邊形綜合題．
【答案】（1）AG=，FG=2；
（2）四邊形ABFG是正方形，理由見解答；
（3）當GM最短時，．
3
3
（2）四邊形ABFG是正方形，理由見解答；
（3）當GM最短時，
GM
=
25
12
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：355引用：3難度：0.1
相似題
-
1．[證明體驗]
（1）如圖1，在△ABC中，點D在邊BC上，點F在邊AC上，AB=AD，FB=FC，AD與BF相交于點E．求證：∠ABF=∠CAD．
[思考探究]
（2）如圖2，在（1）的條件下，過點D作AB的平行線交AC于點G，若DE=2AE，AB=6，求DG的長．
[拓展延伸]
（3）如圖3，在四邊形ABCD中，對角線AC與BD相交于點O，AC⊥AD，∠ABC=∠ACB=67.5°，OD=2OB，OA=，求CD的長．2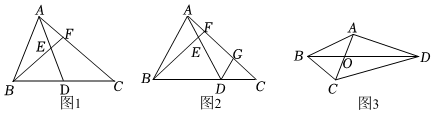
發布：2025/5/23 23:30:1組卷：687引用：3難度：0.3 -
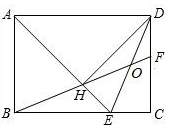2．如圖，在矩形ABCD中，AD=AB，∠BAD的平分線交BC于點E．DH⊥AE于點H，連接BH并延長交CD于點F，連接DE交BF于點O，下列結論：①AD=AE；②∠AED=∠CED；③OE=OD；④BH=HF；⑤BC-CF=2HE，其中正確的有（ ）2發布：2025/5/23 22:30:2組卷：1273引用：4難度：0.2 -
3．【問題提出】
（1）如圖①，OP為∠AOB的平分線，PC⊥OA于點C，PD⊥OB于點D，若S△OPC=3，則S△OPD=
【問題探究】
（2）如圖②，a、b是兩條平行的直線，且a、b之間的距離為12，點A為直線a上一點，點B、C為直線b上兩點，且點B在點C的左側，若∠BAC=45°，求BC的最小值；
【問題解決】
（3）如圖③，四邊形ABCD是園林規劃局欲修建的一塊平行四邊形園林的大致示意圖，沿對角線BD修一條人行走道，沿∠BAD的平分線AP（點P在BD上）修一條園林灌溉水渠．根據規劃要求，∠ABC=120°，AP=120米，且使得平行四邊形ABCD的面積盡可能小，問平行四邊形ABCD的面積是否存在最小值？若存在，求出其最小值，若不存在，請說明理由．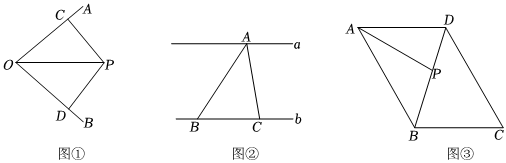
發布：2025/5/23 22:30:2組卷：137引用：1難度：0.2
相關試卷