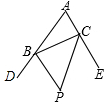
 如圖,BP、CP是△ABC的外角角平分線,若∠P=60°,則∠A的大小為( )
如圖,BP、CP是△ABC的外角角平分線,若∠P=60°,則∠A的大小為( )
【答案】B
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/5/27 14:0:0組卷:2849引用:15難度:0.7
相似題
-
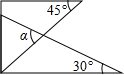 1.如圖是一副三角板疊放的示意圖,則∠α=.發布:2025/6/19 13:0:6組卷:2455引用:64難度:0.5
1.如圖是一副三角板疊放的示意圖,則∠α=.發布:2025/6/19 13:0:6組卷:2455引用:64難度:0.5 -
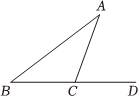 2.如圖,在△ABC中,∠A=30°,∠B=50°,延長BC到D,則∠ACD=°.發布:2025/6/19 13:30:1組卷:638引用:62難度:0.7
2.如圖,在△ABC中,∠A=30°,∠B=50°,延長BC到D,則∠ACD=°.發布:2025/6/19 13:30:1組卷:638引用:62難度:0.7 -
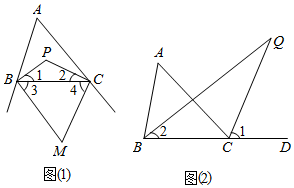 3.探索三角形的內(外)角平分線形成的角的規律
3.探索三角形的內(外)角平分線形成的角的規律
在三角形中,由三角形的內角平分線、外角平分線所形成的角存在一定的規律.
規律1:三角形的兩個內角的平分線形成的鈍角等于90°加上第三個內角度數的一半.
規律2:三角形的兩個外角的平分線形成的銳角等于90°減去與這兩個外角不相鄰的內角度數的一半.
如圖(1),已知點P是△ABC的內角平分線BP與CP的交點,點M是△ABC的外角平分線BM與CM的交點,則∠P=90°+∠A,∠M=90°-12∠A12
證明規律1:
∵BP、CP是△ABC的角平分線,
∴∠1=∠ABC,∠2=12∠ACB,(1)12
∴∠A=180°-2(∠1+∠2),(2)
∴∠1+∠2=90°-∠A,12
∴∠P=180°-(∠1+∠2)=90°+∠A.12
證明規律2:
∵∠3=(∠A+∠ACB),∠4=12(∠A+∠ABC),12
∴∠3+∠4=(∠A+∠ACB+∠ABC)+12∠A=90°+12∠A,12
∴∠M=180°-(∠3+∠4)=90°-∠A.12
請解決以下問題:
(1)寫出上述證明過程中步驟(2)的依據是:;
(2)如圖(2),已知點Q是△ABC的內角平分線BQ與△ABC的外角(∠ACD)平分線CQ的交點,請猜想∠Q和∠A的數量關系,并說明理由.發布:2025/6/19 23:30:1組卷:572引用:2難度:0.7


