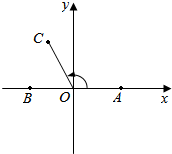
在如圖所示的平面直角坐標系中，已知點A（1，0）和點B（-1，0），|OC|=1，且∠AOC=θ，其中O為坐標原點．
（1）若θ=3π4，設點D為線段OA上的動點，求|OC+OD|的最小值；
（2）若θ∈[0，π2]，向量m=BC，n=（1-cosθ，sinθ-2cosθ），求m?n的最小值及對應的θ值．
|
OC
|
=
1
3
π
4
|
OC
+
OD
|
θ
∈
[
0
，
π
2
]
m
=
BC
，
n
=
（
1
-
cosθ
，
sinθ
-
2
cosθ
）
m
?
n
【答案】（1）；
（2）的最小值為，此時．
2
2
（2）
m
?
n
1
-
2
θ
=
π
8
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：60引用：2難度：0.7
