約翰?開普勒是近代著名的天文學家、數學家、物理學家和哲學家，有一次在上幾何課時，突然想到，一個正三角形的外接圓與內切圓的半徑之比2：1恰好和土星與木星軌道的半徑比很接近，于是他想，是否可以用正多面體的外接球和內切球的半徑比來刻畫太陽系各行星的距離呢？經過實踐，他給出了以下的太陽系模型：最外面一個球面，設定為土星軌道所在的球面，先作一個正六面體內接于此球面，然后作此正六面體的內切球面，它就是木星軌道所在的球面．在此球面中再作一個內接的正四面體，接著作該正四面體的內切球面即得到火星軌道所在的球面，繼續下去，他就得到了太陽系各個行星的模型．根據開普勒的猜想，土星軌道所在的球面與火星軌道所在球面半徑的比值為（ ）
【考點】球的體積和表面積．
【答案】C
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/5 8:0:9組卷：99引用：2難度：0.5
相似題
-
1．大約于東漢初年成書的我國古代數學名著《九章算術》中，“開立圓術”曰：置積尺數，以十六乘之，九而一，所得開立方除之，即立圓徑．“開立圓術”實際是知道了球的體積V，利用球的體積，求其直徑d的一個近似值的公式
，而我們知道，若球的半徑r,則球的體積d=3169V，則在上述公式V=43πr3中，相當于π的取值為（ ）d=3169V發布：2024/12/30 4:0:3組卷：71引用：2難度：0.6 -
2．正方體的表面積與其外接球的表面積的比為（ ）
發布：2024/12/29 12:30:1組卷：9引用：3難度：0.7 -
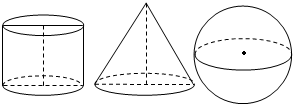3．如圖，一個圓柱和一個圓錐的底面直徑和它們的高都與一個球的直徑2R相等，下列結論正確的是（ ）發布：2024/12/29 9:0:1組卷：354引用：11難度：0.8