數與形是數學研究的兩大部分，它們間的聯系稱為數形結合，數形結合大致分為兩種情形，或者借助圖形的直觀來闡明數之間的關系，或者借助數的精確性來闡明圖形的屬性，即“以形助數”或“以數解形”，整式乘法中也利用圖形面積來論證數量關系．現用磚塊相同的面（如材料圖，長為a,寬為b的小長方形）拼出以下圖形，延長部分邊框，則把這些拼圖置于如圖所示的正方形或大長方形內，請解答下列問題．
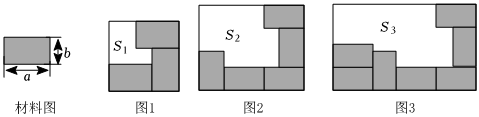
（1）求圖1中空白部分的面積S1（用含a、b的代數式表示）．
（2）圖1，圖2中空白部分面積S1、S2分別為19、68，求ab值．
（3）圖3中空白面積為S3，根據圖形中的數量關系，將下列式子寫成含a、b的整式乘積的形式：
①S3+7ab=（3a+b）（a+2b）（3a+b）（a+2b）；
②S3-a2+5ab=（2a+b）（a+2b）（2a+b）（a+2b）．
S
3
-
a
2
+
5
ab
【考點】完全平方公式的幾何背景．
【答案】（3a+b）（a+2b）；（2a+b）（a+2b）
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/8/16 4:0:1組卷：217引用：3難度：0.5
相似題
-
1．如圖，一個正方形被分成兩個正方形和兩個一模一樣的矩形，請根據圖形，寫出一個含有a,b的正確的等式．發布：2025/5/25 0:30:1組卷：573引用：8難度：0.5 -
2．如圖，將四個小正方形用兩種不同方法放在大正方形的四個頂點，則圖2中陰影部分的面積為（ ）發布：2025/5/25 16:0:2組卷：100引用：1難度：0.7 -
3．靈活運用完全平方公式（a±b）2=a2±2ab+b2可以解決許多數學問題．
例如：已知a-b=3，ab=1，求a2+b2的值．
解：∵a-b=3，ab=1，∴（a-b）2=9，2ab=2，∴a2-2ab+b2=9，∴a2-2+b2=9，∴a2+b2=9+2=11．
請根據以上材料，解答下列問題．
（1）若a2+b2與2ab-4互為相反數，求a+b的值．
（2）如圖，矩形的長為a,寬為b,周長為14，面積為8，求a2+b2的值．發布：2025/5/23 21:0:1組卷：436引用：4難度：0.6