 【閱讀與理解】
【閱讀與理解】
小天同學(xué)看到如下的閱讀材料:
對于一個數(shù)A,以下給出了判斷數(shù)A是否為19的倍數(shù)的一種方法:
每次劃掉該數(shù)的最后一位數(shù)字,將劃掉這個數(shù)字的兩倍與剩下的數(shù)相加得到一個和,稱為一次操作,以此類推,直到數(shù)變?yōu)?0以內(nèi)的數(shù)為止.若最后得到的數(shù)為19.則最初的數(shù)A就是19的倍數(shù),否則,數(shù)A就不是19的倍數(shù).
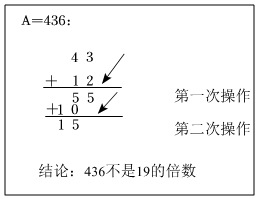
以A=436為例,如右面算式所示,經(jīng)過第一次操作得到55,經(jīng)過第二次操作得到15,15<20,15≠19.所以436不是19的倍數(shù).
當(dāng)數(shù)A的位數(shù)更多時,這種方法依然適用.
【操作與說理】
(1)當(dāng)A=532時,請你幫小天寫出判斷過程;
(2)小天嘗試說明方法的道理,他發(fā)現(xiàn)解決問題的關(guān)鍵是每次判斷過程的第一次操作,后續(xù)的操作道理都與第一次相同,于是他列出了如下表格進(jìn)行分析.請你補(bǔ)全小天列出的表格:
說明:abc表示100a+10b+c,其中1≤a≤9,0≤b≤9,0≤c≤9,a,b,c均為整數(shù).
abc
| A | A的表達(dá)式 | 第一次操作得到的和,記為M(A) |
| 436 | 436=10×43+6 | M(436)=43+2×6 |
| 532 | 532= 10×53+2 10×53+2 |
M(532)= 53+2×2 53+2×2 |
| 863 | 863=10×86+3 | M(863)=86+2×3 |
| … | … | … |
abc |
abc 100a+10b+c 100a+10b+c |
M( abc 10a+b+2c 10a+b+2c |
abc
abc
【考點】因式分解的應(yīng)用.
【答案】10×53+2;53+2×2;100a+10b+c;10a+b+2c
【解答】
【點評】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/10/5 13:0:1組卷:486引用:2難度:0.5
相似題
-
1.已知a,b,c為△ABC的三條邊的長,
(1)當(dāng)b2+2ab=c2+2ac時,試判斷△ABC屬于哪一類三角形;
(2)判斷a2-b2-2bc-c2的值的符號,并說明理由.發(fā)布:2025/7/1 13:0:6組卷:207引用:1難度:0.3 -
2.已知:a>b>0,且a2+b2=
ab,那么103的值為b+ab-a.發(fā)布:2025/6/25 7:30:2組卷:719引用:4難度:0.9 -
3.若a2-ab=7-m,b2-ab=9+m,則a-b的值為( )
A.2 B.±2 C.4 D.±4 發(fā)布:2025/6/25 6:0:1組卷:581引用:2難度:0.7


