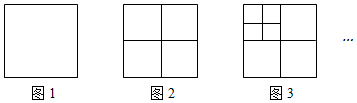
如圖1，給定一個正方形，要通過畫線將其分割成若干個互不重疊的正方形．第1次畫線分割成4個互不重疊的正方形，得到圖2；第2次畫線分割成7個互不重疊的正方形，得到圖3……以后每次只在上次得到圖形的左上角的正方形中畫線．
嘗試：第3次畫線后，分割成1010個互不重疊的正方形；
第4次畫線后，分割成1313個互不重疊的正方形．
發現：第n次畫線后，分割成（3n+1）（3n+1）個互不重疊的正方形；并求第2020次畫線后得到互不重疊的正方形的個數．
探究：若干次畫線后，能否得到1001個互不重疊的正方形？若能，求出是第幾次畫線后得到的；若不能，請說明理由．
【考點】規律型：圖形的變化類．
【答案】10；13；（3n+1）
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/7 5:0:1組卷：313引用：4難度：0.7
相似題
-
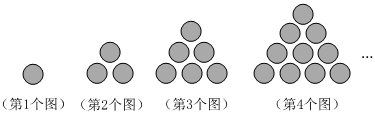
1．如圖都是由同樣大小的小球按一規律排列的，依照此規律排列下去，第5個圖共有 個小球，第 圖形共有210小球．
發布：2025/6/7 6:30:1組卷：13引用：1難度：0.6 -
2．按如圖所示的規律搭正方形：搭一個小正方形需要4根小棒，搭兩個小正方形需要7根小棒，搭2022個這樣的小正方形需要小棒（ ）根．
發布：2025/6/7 7:0:1組卷：108引用：4難度：0.6 -
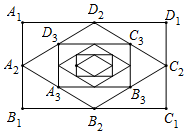3．如圖：順次連接矩形A1B1C1D1四邊的中點得到四邊形A2B2C2D2，再順次連接四邊形A2B2C2D2四邊的中點得四邊形A3B3C3D3，…，按此規律得到四邊形AnBnCnDn．若矩形A1B1C1D1的面積為8，那么四邊形AnBnCnDn的面積為．發布：2025/6/7 10:30:1組卷：268引用：5難度：0.5