先閱讀,再解題:因為1-12=11×2,12-13=12×3,13-14=13×4,…
所以11×2+12×3+13×4+…+149×50=(1-12)+(12-13)+(13-14)+…+(149-150)
=1-12+12-13+13-14+…+149-150
=1-150
=4950.
參照上述解法計算:11×3+13×5+15×7+…+12019×2021.
1
-
1
2
=
1
1
×
2
,
1
2
-
1
3
=
1
2
×
3
1
3
-
1
4
=
1
3
×
4
1
1
×
2
+
1
2
×
3
+
1
3
×
4
+
…
+
1
49
×
50
=
(
1
-
1
2
)
+
(
1
2
-
1
3
)
+
(
1
3
-
1
4
)
+
…
+
(
1
49
-
1
50
)
1
-
1
2
+
1
2
-
1
3
+
1
3
-
1
4
+
…
+
1
49
-
1
50
1
-
1
50
49
50
1
1
×
3
+
1
3
×
5
+
1
5
×
7
+
…
+
1
2019
×
2021
【考點】規律型:數字的變化類;有理數的混合運算.
【答案】.
1010
2021
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/27 10:35:59組卷:180引用:1難度:0.5
相似題
-
1.觀察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…,則2+22+23+24+?+22022+22023的末位數字是 .
發布:2025/5/30 10:30:1組卷:77引用:3難度:0.7 -
2.如圖所示,在這個數據運算程序中,若開始輸入的x的值為5,第1次運算結果輸出的是8,返回進行第二次運算輸出的是4,…,則第2023次輸出的結果是( )
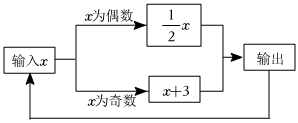
A.1 B.2 C.4 D.8 發布:2025/5/30 12:0:2組卷:124引用:2難度:0.7 -
3.a是不為1的有理數,我們把
稱為a的差倒數.如:2的差倒數是11-a,-1的差倒數是11-2=-1.已知11-(-1)=12,a2是a1的差倒數,a3是a2的差倒數,a4是a3的差的倒數,…,以此類推,則a3=,a2022的差倒數a2023=.a1=-13發布:2025/5/30 10:30:1組卷:80引用:1難度:0.6


