[概念引入]
在一個圓中，圓心到該圓的任意一條弦的距離，叫做這條弦的弦心距．
[概念理解]
（1）如圖1，在⊙O中，半徑是5，弦AB=8，則這條弦的弦心距OC長為 33．
（2）通過大量的做題探究；小明發現：在同一個圓中，如果兩條弦相等，那么這兩條弦的弦心距也相等．但是小明想證明時卻遇到了麻煩．請結合圖2幫助小明完成證明過程如圖2，在⊙O中，AB=CD，OM⊥AB，ON⊥CD，求證：OM=ON．
[概念應用]如圖3，在⊙O中AB=CD=16，⊙O的直徑為20，且弦AB垂直于弦CD于E，請應用上面得出的結論求OE的長．
【考點】圓的綜合題．
【答案】3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：313引用：6難度：0.3
相似題
-
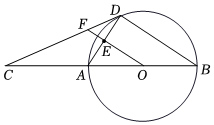1．如圖，AB為⊙O的直徑，點C在BA延長線上，點D在⊙O上，連接CD，AD，∠ADC=∠B，OF⊥AD于點E，交CD于點F．
（1）求證：CD是⊙O的切線；
（2）若S△COF：S△CBD=9：16，求sinC的值．發布：2025/5/23 18:30:2組卷：300引用：1難度：0.4 -
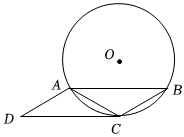2．如圖，⊙O是△ABC的外接圓，分別過A，C作AD∥BC，CD∥AB．
（1）求證：AD=BC；
（2）若AC=BC．
①求證：CD是⊙O的切線；
②已知AB=6cm,當四邊形ABCD的某條邊所在直線過圓心O時，求⊙O的半徑．發布：2025/5/23 17:30:1組卷：150引用：2難度：0.1 -
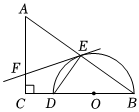3．如圖，在△ABC中，∠C=90°，AC=3，BC=4．O為BC邊上一點，以O為圓心，OB為半徑作半圓，分別于與邊BC、AB交于點D、E，連接DE．
（1）∠BED=°；
（2）當BD=3時，求DE的長；
（3）過點E作半圓O的切線，當切線與邊AC相交時，設交點為F．求證：AF=EF．發布：2025/5/23 17:30:1組卷：229引用：4難度：0.1