如圖，直線AB與x軸交于A（-3，0），與y軸交于點B（0，-33）．點Q是線段AB上的動點，過Q作直線l∥x軸，直線l與∠OAB的平分線交于點M，與∠BAx的平分線交于點N．
（1）當AB=3AQ時，求MN的長；
（2）定點C（-2，0），連接CQ，求CQ+12BQ的最小值；
（3）當MN=23時，將△AMN沿著射線AB平移得到△A′M′N′，邊A′M′所在的直線與y軸交于D點，若△DM′N′是等腰三角形時，直接寫出OD的長．
B
（
0
，-
3
3
）
1
2
3
【考點】幾何變換綜合題．
【答案】（1）MN=4；
（2）；
（3）OD=3或5-3或3+3．
（2）
7
2
（3）OD=3
3
-
1
3
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：150引用：1難度：0.1
相似題
-
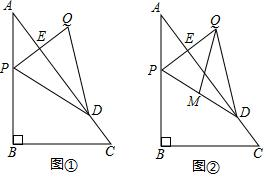1．如圖①，在△ABC中，∠ABC=90°，AB=4，BC=3．點P從點A出發，沿折線AB-BC以每秒5個單位長度的速度向點C運動，同時點D從點C出發，沿CA以每秒2個單位長度的速度向點A運動，點P到達點C時，點P、D同時停止運動．當點P不與點A、C重合時，作點P關于直線AC的對稱點Q，連接PQ交AC于點E，連接DP、DQ．設點P的運動時間為t秒，線段CE的長為y.
（1）求出y與t之間的函數關系式；
（2）當△PDQ為銳角三角形時，求t的取值范圍；
（3）如圖②，取PD的中點M，連接QM．當直線QM與△ABC的一條直角邊平行時，直接寫出t的值．發布：2025/5/26 8:0:5組卷：371引用：1難度：0.1 -
2．如圖，兩直角三角形ABC和DEF有一條邊BC與EF在同一直線上，且∠DFE=∠ACB=60°，BC=1，EF=2．設EC=m（0≤m≤4），點M在線段AD上，且∠MEB=60°．
（1）如圖1，當點C和點F重合時，=；AMDM
（2）如圖2，將圖1中的△ABC繞點C逆時針旋轉，當點A落在DF邊上時，求的值；AMDM
（3）當點C在線段EF上時，△ABC繞點C逆時針旋轉α度（0＜α＜90°），原題中其他條件不變，則=．AMDM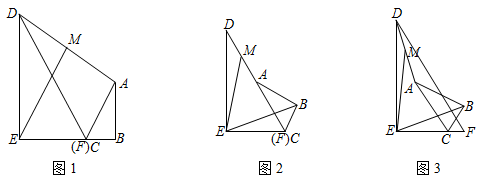
發布：2025/5/26 11:0:2組卷：652引用：2難度：0.2 -
3．在△ABC中，AC=AB，∠CAB=120°，點D是邊AB上的一動點．F是邊CD上的動點．連接AF并延長至點E，交BC于G，連接BE．且∠E+∠BDF=180°，∠AFC=60°．
（1）如圖1，若BC=6，BE=4，求CD的長．3
（2）如圖2，若點D是AB的中點，求證：AE=DF+BF．3
（3）如圖3，在（2）的條件下，將△BDE繞點B順時針旋轉，旋轉中的三角形記作△D1BE1，取D1E1的中點為M，連接CM．當CM最大時，直接寫出的值．AM2EM2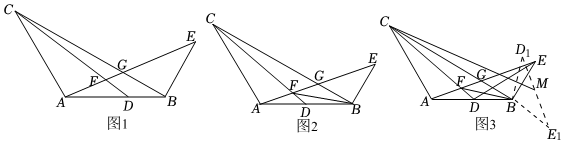
發布：2025/5/26 11:30:1組卷：164引用：1難度：0.1