體育課上，小明和小聰突然爭論起來，他們都說自己比對(duì)方身體長的高，這時(shí)善于思考的小慧走過來，笑著對(duì)他倆說：“你們不要爭了，其實(shí)你們一樣高，看看地上，你倆的影子一樣長”（假設(shè)太陽光線是平行的）．小明和小聰不太明白，小慧給他們講了其中的道理．
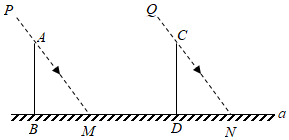
小慧說我們先對(duì)該問題進(jìn)行數(shù)學(xué)抽象：如圖，直線a表示地面，AB，CD分別表示你倆的身高，PM和QN表示太陽光線，是平行的，BM和DN表示你倆身高的影長，是一樣長的．然后小慧用所學(xué)的數(shù)學(xué)知識(shí)解決了該問題．
下面給出了小慧解決該問題的一部分內(nèi)容，請(qǐng)你將已知，求證補(bǔ)充完整，并給出證明：
（1）已知：如圖，AB⊥a于點(diǎn)B，CD⊥a于點(diǎn)D，AM∥CN，或PM∥QNAM∥CN，或PM∥QN，BM=DNBM=DN；
（2）求證：AB=CDAB=CD；
（3）證明：∵AB⊥a,CD⊥a,
∴∠ABM=∠CDN=90°．
∵AM∥CN，
∴∠AMB=∠CND
∵BM=DN，
在△ABM與△CDN中，
∠ABM=∠CDN BM=DN ∠AMB=∠CND
，
∴△ABM≌△CDN（ASA）．
∴AB=CD∵AB⊥a,CD⊥a,
∴∠ABM=∠CDN=90°．
∵AM∥CN，
∴∠AMB=∠CND
∵BM=DN，
在△ABM與△CDN中，
∠ABM=∠CDN BM=DN ∠AMB=∠CND
，
∴△ABM≌△CDN（ASA）．
∴AB=CD．
∴∠ABM=∠CDN=90°．
∵AM∥CN，
∴∠AMB=∠CND
∵BM=DN，
在△ABM與△CDN中，
∠ ABM =∠ CDN |
BM = DN |
∠ AMB =∠ CND |
∴△ABM≌△CDN（ASA）．
∴AB=CD
∴∠ABM=∠CDN=90°．
∵AM∥CN，
∴∠AMB=∠CND
∵BM=DN，
在△ABM與△CDN中，
∠ ABM =∠ CDN |
BM = DN |
∠ AMB =∠ CND |
∴△ABM≌△CDN（ASA）．
∴AB=CD
【考點(diǎn)】全等三角形的應(yīng)用；平行投影．
【答案】AM∥CN，或PM∥QN；BM=DN；AB=CD；∵AB⊥a，CD⊥a，
∴∠ABM=∠CDN=90°．
∵AM∥CN，
∴∠AMB=∠CND
∵BM=DN，
在△ABM與△CDN中，
，
∴△ABM≌△CDN（ASA）．
∴AB=CD
∴∠ABM=∠CDN=90°．
∵AM∥CN，
∴∠AMB=∠CND
∵BM=DN，
在△ABM與△CDN中，
∠ ABM =∠ CDN |
BM = DN |
∠ AMB =∠ CND |
∴△ABM≌△CDN（ASA）．
∴AB=CD
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/4/20 14:35:0組卷：83引用：2難度：0.5
相似題
-
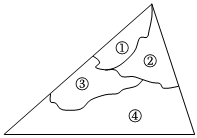1．如圖，某同學(xué)把一塊三角形的玻璃打碎成了四塊，現(xiàn)在要到玻璃店配一塊完全一樣的玻璃，那么最省事的辦法是（ ）發(fā)布：2025/6/1 19:30:1組卷：227引用：3難度：0.5 -
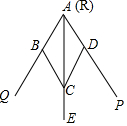2．如圖，小敏做了一個(gè)角平分儀ABCD，其中AB=AD，BC=DC，將儀器上的點(diǎn)A與∠PRQ的頂點(diǎn)R重合，調(diào)整AB和AD，使它們分別落在角的兩邊上，過點(diǎn)A，C畫一條射線AE，AE就是∠PRQ的平分線．此角平分儀的畫圖原理是：根據(jù)儀器結(jié)構(gòu)，可得△ABC≌△ADC，這樣就有∠QAE=∠PAE．則說明這兩個(gè)三角形全等的依據(jù)是．發(fā)布：2025/6/1 17:30:1組卷：973引用：9難度：0.9 -
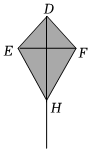3．“三月三，放風(fēng)箏”，如圖是小明制作的風(fēng)箏，他根據(jù)DE=DF，EH=FH，不用測(cè)量，就知道∠DEH=∠DFH，小明是通過全等三角形的知識(shí)得到的結(jié)論，則小明判定三角形全等的依據(jù)是 （用字母表示）．發(fā)布：2025/6/2 1:30:2組卷：420引用：8難度：0.6