“黃金分割”給人以美感，它在建筑、藝術(shù)等領(lǐng)域有著廣泛的應(yīng)用．如圖1，點B把線段AC分成兩部分，如果BCAB=ABAC，那么稱線段AC被點B黃金分割，點B為線段AC的黃金分割點．AB與AC的比稱為黃金比，它們的比值為5-12．請在圖2中完成相應(yīng)的問題：
已知，∠MON=60°，點A在OM邊上，OA=4．
（1）請在ON邊上用無刻度的直尺和圓規(guī)作出點B，使得OB與OA的比為黃金比；（不寫作法，保留作圖痕跡）
（2）△AOB的面積=215-23215-23．
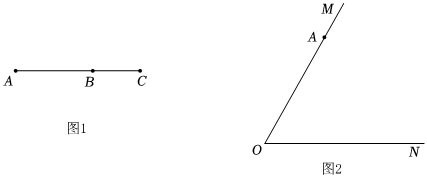
BC
AB
=
AB
AC
5
-
1
2
2
15
-
2
3
2
15
-
2
3
【答案】
2
15
-
2
3
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/5/23 15:30:2組卷：1527引用：2難度：0.4
相似題
-
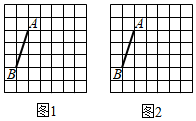1．如圖，在“7×7”的方格中，每個小正方形的邊長均為1，線段AB的兩個端點均在格點上（在小方格頂點上的點稱為格點），按如下要求畫圖：
（1）在圖1中畫一個以線段AB為對角線的平行四邊形ACBD，要求點C，D在格點上，平行四邊形ACBD的面積為6；
（2）在圖2中畫一個以線段AB為邊的平行四邊形ABEF，要求點E，F(xiàn)在格點上，平行四邊形ABEF有一個內(nèi)角的度數(shù)為45°．發(fā)布：2025/5/23 23:30:1組卷：213引用：3難度：0.5 -
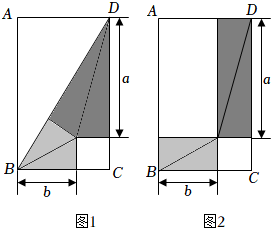2．利用圖形的分、和、移、補(bǔ)探索圖形關(guān)系，是我國傳統(tǒng)數(shù)學(xué)的一種重要方法．如圖1，BD是矩形ABCD的對角線，將△BCD分割成兩對全等的直角三角形和一個正方形，然后按圖2重新擺放，觀察兩圖，若a=4，b=2，則矩形ABCD的面積是 ．發(fā)布：2025/5/24 1:0:1組卷：2443引用：20難度：0.4 -
3．如圖，在每個小正方形的邊長為1的網(wǎng)格中，△ABC的頂點A在格點上，B是小正方形邊的中點，∠ABC=50°，∠BAC=30°，經(jīng)過點A，B的圓的圓心在邊AC上．
（1）線段AB的長等于 ；
（2）請用無刻度的直尺，在如圖所示的圓上，畫出一個點D，使其滿足∠ADB的度數(shù)小于∠ACB的度數(shù)，并說明理由；
（3）請用無刻度的直尺，在如圖所示的網(wǎng)格中，畫出一個點P，使其滿足∠PAC=∠PBC=∠PCB，并簡要說明點P的位置是如何找到的（不要求證明） ．
發(fā)布：2025/5/24 3:0:1組卷：160引用：3難度：0.4