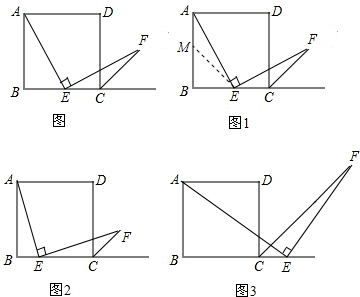
如圖(*),四邊形ABCD是正方形,點E是邊BC的中點,∠AEF=90°,且EF交正方形外角平分線CF于點F.請你認真閱讀下面關于這個圖的探究片段,完成所提出的問題.
(1)探究1:小強看到圖(*)后,很快發現AE=EF,這需要證明AE和EF所在的兩個三角形全等,但△ABE和△ECF顯然不全等(一個是直角三角形,一個是鈍角三角形),考慮到點E是邊BC的中點,因此可以選取AB的中點M,連接EM后嘗試著去證△AEM≌EFC就行了,隨即小強寫出了如下的證明過程:
證明:如圖1,取AB的中點M,連接EM.
∵∠AEF=90°
∴∠FEC+∠AEB=90°
又∵∠EAM+∠AEB=90°
∴∠EAM=∠FEC
∵點E,M分別為正方形的邊BC和AB的中點
∴AM=EC
又可知△BME是等腰直角三角形
∴∠AME=135°
又∵CF是正方形外角的平分線
∴∠ECF=135°
∴△AEM≌△EFC(ASA)
∴AE=EF
(2)探究2:小強繼續探索,如圖2,若把條件“點E是邊BC的中點”改為“點E是邊BC上的任意一點”,其余條件不變,發現AE=EF仍然成立,請你證明這一結論.
(3)探究3:小強進一步還想試試,如圖3,若把條件“點E是邊BC的中點”改為“點E是邊BC延長線上的一點”,其余條件仍不變,那么結論AE=EF是否成立呢?若成立請你完成證明過程給小強看,若不成立請你說明理由.
【考點】正方形的性質;全等三角形的判定與性質.
【答案】見試題解答內容
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/27 10:35:59組卷:3738引用:8難度:0.3
相似題
-
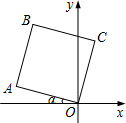 1.將邊長為2的正方形OABC如圖放置,O為原點.若∠α=15°,則點B的坐標為.發布:2025/6/8 1:30:1組卷:360引用:14難度:0.7
1.將邊長為2的正方形OABC如圖放置,O為原點.若∠α=15°,則點B的坐標為.發布:2025/6/8 1:30:1組卷:360引用:14難度:0.7 -
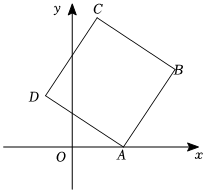 2.如圖,在平面直角坐標系中,已知點A(2,0),D(-1,2),且四邊形ABCD為正方形,則點C的坐標為( )
2.如圖,在平面直角坐標系中,已知點A(2,0),D(-1,2),且四邊形ABCD為正方形,則點C的坐標為( )A. (12,5)B. (5,12)C.(5,1) D.(1,5) 發布:2025/6/8 1:0:1組卷:84引用:3難度:0.6 -
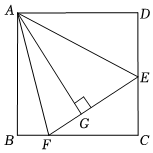 3.如圖,點E、F分別在正方形ABCD的邊DC、BC上,AG⊥EF,垂足為G,且AG=AB,則∠EAF=( )
3.如圖,點E、F分別在正方形ABCD的邊DC、BC上,AG⊥EF,垂足為G,且AG=AB,則∠EAF=( )A.30° B.45° C.50° D.60° 發布:2025/6/8 1:30:1組卷:518引用:3難度:0.5


