2021-2022學年四川省德陽二中八年級（下）期中數學試卷
發(fā)布：2024/4/20 14:35:0
一、選擇題，下列各題中只有一個選項是正確的，請將正確答案的番號選填在答卷相應題號內。（本大題共12個小題，每題4分，共48分）
-
1．下列各組數是勾股數的是（ ）
組卷：415引用：5難度：0.9 -
2．在直角坐標系中，點P（2，-3）到原點的距離是（ ）
組卷：1647引用：8難度：0.9 -
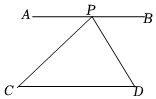3．如圖，直線AB∥CD，P是AB上的動點，當點P的位置變化時，三角形PCD的面積將（ ）組卷：193引用：4難度：0.7 -
4．如圖，數軸上的點A所表示的數為x,則x的值為（ ）
組卷：1079引用：17難度：0.9 -
5．已知三角形的三邊長為a、b、c,如果（a-5）2+|b-12|+（c-13）2=0，則△ABC是（ ）
組卷：864引用：2難度：0.5 -
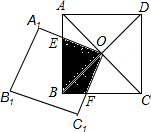6．如圖，正方形ABCD的對角線交于點O，點O又是正方形A1B1C1O的一個頂點，而且這兩個正方形的邊長相等．無論正方形A1B1C1O繞點O怎樣轉動，兩個正方形重疊部分的面積，總等于一個正方形面積的（ ）組卷：718引用：8難度：0.9 -
7．數學興趣小組開展以下折紙活動：
（1）對折矩形ABCD，使AD和BC重合，得到折痕EF，把紙片展平；
（2）再一次折疊紙片，使點A落在EF上，并使折痕經過點B，得到折痕BM，同時得到線段BN．
觀察，探究可以得到∠ABM的度數是（ ）組卷：1977引用：48難度：0.9 -
8．下列說法正確的有（ ）
①對角線互相平分的四邊形是平行四邊形
②對角線相等的四邊形是矩形
③對角線互相垂直的四邊形是菱形
④對角線相等的平行四邊形是矩形
⑤對角線互相垂直且相等的平行四邊形是正方形組卷：329引用：2難度：0.7
三、解答題（本大題有6小題，共74分，解答要求寫出文字說明，證明過程或計算步驟）
-
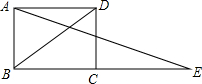24．如圖，延長矩形ABCD的邊BC至點E，使CE=BD，連接AE．
（1）若∠ADB=40°，求∠E的度數．
（2）若AB=3，CE=5，求AE的長．組卷：327引用：3難度：0.5 -
25．如圖（*），四邊形ABCD是正方形，點E是邊BC的中點，∠AEF=90°，且EF交正方形外角平分線CF于點F．請你認真閱讀下面關于這個圖的探究片段，完成所提出的問題．
（1）探究1：小強看到圖（*）后，很快發(fā)現(xiàn)AE=EF，這需要證明AE和EF所在的兩個三角形全等，但△ABE和△ECF顯然不全等（一個是直角三角形，一個是鈍角三角形），考慮到點E是邊BC的中點，因此可以選取AB的中點M，連接EM后嘗試著去證△AEM≌EFC就行了，隨即小強寫出了如下的證明過程：
證明：如圖1，取AB的中點M，連接EM．
∵∠AEF=90°
∴∠FEC+∠AEB=90°
又∵∠EAM+∠AEB=90°
∴∠EAM=∠FEC
∵點E，M分別為正方形的邊BC和AB的中點
∴AM=EC
又可知△BME是等腰直角三角形
∴∠AME=135°
又∵CF是正方形外角的平分線
∴∠ECF=135°
∴△AEM≌△EFC（ASA）
∴AE=EF
（2）探究2：小強繼續(xù)探索，如圖2，若把條件“點E是邊BC的中點”改為“點E是邊BC上的任意一點”，其余條件不變，發(fā)現(xiàn)AE=EF仍然成立，請你證明這一結論．
（3）探究3：小強進一步還想試試，如圖3，若把條件“點E是邊BC的中點”改為“點E是邊BC延長線上的一點”，其余條件仍不變，那么結論AE=EF是否成立呢？若成立請你完成證明過程給小強看，若不成立請你說明理由．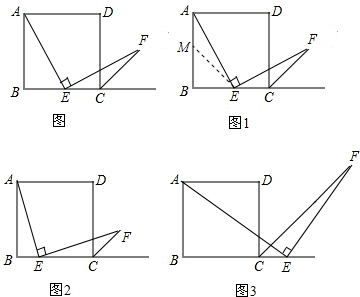
組卷：3737引用：8難度：0.3