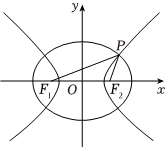
已知橢圓C1：x2a21+y2b21=1（a1＞b1＞0）與雙曲線C2：x2a22-y2b22=1（a2＞b2＞0）有相同的焦點F1、F2，橢圓C1的離心率為e1，雙曲線C2的離心率為e2，點P為橢圓C1與雙曲線C2的交點，且∠F1PF2=π3，則1e21+3e22的值為（ ）
C
1
：
x
2
a
2
1
+
y
2
b
2
1
=
1
（
a
1
＞
b
1
＞
0
）
C
2
：
x
2
a
2
2
-
y
2
b
2
2
=
1
（
a
2
＞
b
2
＞
0
）
∠
F
1
P
F
2
=
π
3
1
e
2
1
+
3
e
2
2
【答案】D
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/8/9 8:0:9組卷：337引用：6難度：0.7
相關(guān)試卷