如圖所示，四邊形OABC為正方形，邊長為6，點A，C分別在x軸，y軸的正半軸上，點D在OA上，且D的坐標為（2，0），P是OB上的一動點，試求PD+PA和的最小值是（　　）

A．2

B．

C．4

D．6

【答案】A

【解答】

【點評】

聲明：本試題解析著作權屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。

發(fā)布：2024/4/20 14:35:0組卷：891引用：34難度：0.5

相似題

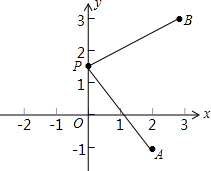1．平面直角坐標系內(nèi)有A（2，-1），B（3，3）兩點，點P是y軸上一動點，求P到A、B距離之和最小時的坐標．
發(fā)布：2025/5/27 21:0:1組卷：157引用：3難度：0.5
解析
2．已知實數(shù)a、b滿足條件a＞0，b＞0，且a+b=4，則代數(shù)式
a
2
+
1
+
b
2
+
4
的最小值是

．
發(fā)布：2025/5/27 22:0:2組卷：273引用：1難度：0.5
解析
3．在邊長為1的正方形ABCD中，點M、N、O、P分別在邊AB、BC、CD、DA上．如果AM=BM，DP=3AP，則MN+NO+OP的最小值是

．
發(fā)布：2025/5/27 21:0:1組卷：109引用：1難度：0.7
解析

相關試卷

1．平面直角坐標系內(nèi)有A（2，-1），B（3，3）兩點，點P是y軸上一動點，求P到A、B距離之和最小時的坐標．