問題探究
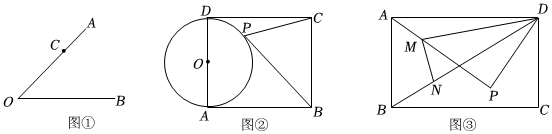
（1）如圖①，已知∠AOB=45°，點C是OA上一點，OC=6，則點C到OB的距離為 3232；
（2）如圖②，在矩形ABCD中，AB=4，BC=3，AD是⊙O的直徑，P是⊙O上任意一點，求△PBC面積的最小值；
問題解決
（3）如圖③，矩形ABCD是某景區(qū)的一處景觀示意圖，其中AB=1003m,BC=300m，連接BD．現(xiàn)欲在該景觀內(nèi)建一觀景亭P，AP與DP是兩條夾角為90°的觀景小道（即∠APD=90°），點M在AP上且DP=MP，點N是BD上一點．為了美觀大方，管理員計劃沿線段MN、NB安裝彩燈，BN段安裝彩燈所需費用為a元/米，MN段安裝彩燈所需費用為2a元/米，請問沿線段MN、NB安裝彩燈至少要花費多少元？（用含a的式子表示）
2
2
AB
=
100
3
m
,
BC
=
300
m
【考點】圓的綜合題．
【答案】3
2
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：81引用：1難度：0.3
相似題
-
1．若AC=4，以點C為圓心，2為半徑作圓，點P為該圓上的動點，連接AP．
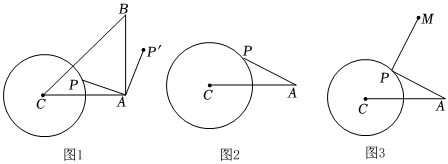
（1）如圖1，取點B，使△ABC為等腰直角三角形，∠BAC=90°，將點P繞點A順時針旋轉(zhuǎn)90°得到AP′．
①點P'的軌跡是 （填“線段”或者“圓”）；
②CP'的最小值是 ；
（2）如圖2，以AP為邊作等邊△APQ（點A、P、Q按照順時針方向排列），在點P運動過程中，求CQ的最大值．
（3）如圖3，將點A繞點P逆時針旋轉(zhuǎn)90°，得到點M，連接PM，則CM的最小值為 ．發(fā)布：2025/5/24 11:30:1組卷：521引用：2難度：0.3 -
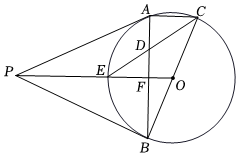2．如圖，PA、PB是⊙O的切線，切點分別為A、B，BC是⊙O的直徑，PO交⊙O于E點，連接AB交PO于F，連接CE交AB于D點．下列結(jié)論：①PA=PB；②OP⊥AB；③CE平分∠ACB；④；⑤E是△PAB的內(nèi)心；⑥△CDA≌△EDF．其中一定成立的有（ ）個．OF=12AC發(fā)布：2025/5/24 12:0:1組卷：489引用：2難度：0.3 -
3．如圖1，CD是⊙O的弦，半徑OA⊥CD，垂足為B，過點C作⊙O的切線l.
（1）若點E在⊙O上，且=?CE，連接OE．?CA
①連接AE，求證：AE∥l；
②如圖2，若B是OA的中點，連接OD，求證：DE是⊙O的直徑；
（2）如圖3，過點B作BF⊥l,垂足為F，若⊙O的半徑是4，求BC-BF的最大值．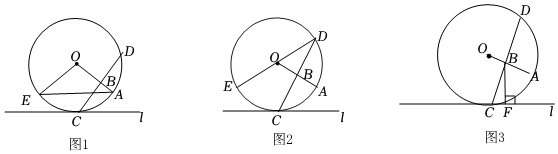
發(fā)布：2025/5/24 11:0:1組卷：345引用：3難度：0.3
相關(guān)試卷