 已知點P和非零實數(shù)λ,若兩條不同的直線l1,l2均過點P,且斜率之積為λ,則稱直線l1,l2是一組“Pλ共軛線對”,如直線l1:y=2x和l2:y=-12x是一組“O-1共軛線對”,其中O是坐標原點.
已知點P和非零實數(shù)λ,若兩條不同的直線l1,l2均過點P,且斜率之積為λ,則稱直線l1,l2是一組“Pλ共軛線對”,如直線l1:y=2x和l2:y=-12x是一組“O-1共軛線對”,其中O是坐標原點.
(1)已知l1、l2是一組“O-3共軛線對”,求l1,l2的夾角的最小值;
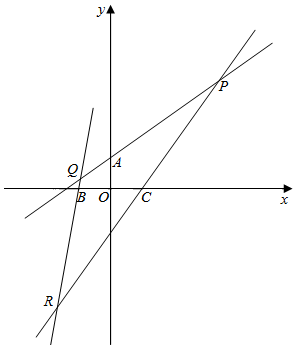
(2)已知點A(0,1)、點B(-1,0)和點C(1,0)分別是三條直線PQ,QR,RP上的點(A,B,C與P,Q,R均不重合),且直線PR,PQ是“P1共軛線對”,直線QP,QR是“Q4共軛線對”,直線RP,RQ是“R9共軛線對”,求點P的坐標;
(3)已知點Q(-1,-2),直線l1,l2是“Q-2共軛線對”,當l1的斜率變化時,求原點O到直線l1、l2的距離之積的取值范圍.
-
1
2
x
2
【答案】見試題解答內(nèi)容
【解答】
【點評】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/6/27 10:35:59組卷:230引用:9難度:0.5
相似題
-
1.若方程組
的解集為{(2,1)},則( )ax+y=2x+by=2A.a(chǎn)=0,b=0 B. ,b=0a=12C.a(chǎn)=0, b=12D. ,a=12b=12發(fā)布:2024/10/7 6:0:2組卷:57引用:1難度:0.9 -
2.已知P1(a1,b1)與P2(a2,b2)是直線y=kx+2(k為常數(shù))上兩個不同的點,則關(guān)于l1:a1x+b1y-2=0和l2:a2x+b2y-2=0的交點情況是( )
A.無論k,P1,P2如何,總有唯一交點 B.存在k,P1,P2使之有無窮多個交點 C.無論k,P1,P2如何,總是無交點 D.存在k,P1,P2使之無交點 發(fā)布:2024/11/16 5:30:1組卷:548引用:6難度:0.7 -
3.已知三條直線l1:x-2y+2=0,l2:x-2=0,l3:x+ky=0將平面分為六個部分,則滿足條件的k的值共有( )
A.1個 B.2 個 C.3個 D.無數(shù)個 發(fā)布:2024/12/14 20:30:1組卷:996引用:7難度:0.7


