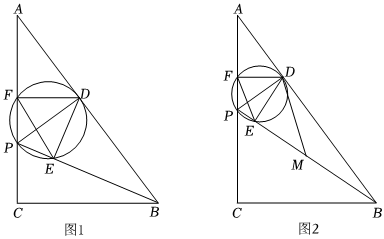
如圖1，在Rt△ABC中，∠C=90°，BC=3，AB=5，點P為AC上一點，PD⊥AB于點D，連結PB，以PD為直徑的圓交BP于點E，交AC于點F，連結DE，DF，EF．
（1）求證：∠DEF=∠ABC；
（2）當△DEF為等腰三角形時，求所有滿足條件的AP的長；
（3）如圖2，過D作DM∥EF交PB于點M，若點M為PB的中點，則DM=151026151026．（直接寫出答案）
15
10
26
15
10
26
【考點】圓的綜合題．
【答案】
15
10
26
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：87引用：1難度：0.3
相似題
-
1．如圖，⊙O的半徑為5，弦BC=6，A為BC所對優弧上一動點，△ABC的外角平分線AP交⊙O于點P，直線AP與直線BC交于點E．
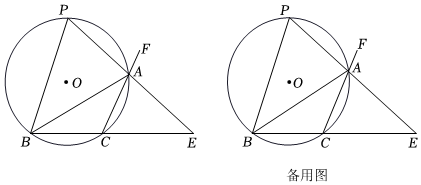
（1）求證：P為優弧BAC的中點；
（2）連接PC，求PC的長度；
（3）求sin∠BAC的值；
（4）若△ABC為非銳角三角形，請直接寫出△ABC的面積的最大值．發布：2025/6/15 3:0:1組卷：97引用：1難度：0.1 -
2．【數學概念】
有一條對角線平分一組對角的四邊形叫“對分四邊形”．
【概念理解】
（1）關于“對分四邊形”，下列說法正確的是 ．（填所有正確的序號）
①菱形是“對分四邊形”
②“對分四邊形”至少有兩組鄰邊相等
③“對分四邊形”的對角線互相平分
【問題解決】
（2）如圖①，PA為⊙O的切線，A為切點．在⊙O上是否存在點B、C，使以P、A、B、C為頂點的四邊形是“對分四邊形”？
請根據小明的作法補全圖形，并證明四邊形PACB是“對分四邊形”．小明的作法：
①以P為圓心，PA長為半徑作弧，與⊙O交于點B；
②連接PO并延長，交⊙O于點C；
③點B、C即為所求．
（3）如圖②，已知線段AB和直線l,請在圖②中利用無刻度的直尺和圓規，在直線l上作出點M、N，使以A、B、M、N為頂點的四邊形是“對分四邊形”．（只要作出一個即可，不寫作法，保留作圖痕跡）
（4）如圖③，⊙O的半徑為5，AB是⊙O的弦，AB=8，點C是⊙O上的動點，若存在四邊形ABCD是“對分四邊形”，且有一條邊所在的直線是⊙O的切線，直接寫出AC的長度．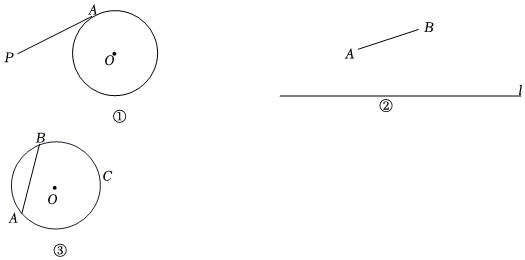
發布：2025/6/14 20:30:2組卷：977引用：3難度：0.1 -
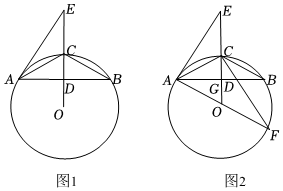3．如圖，⊙O為△ABC的外接圓，AC=BC，D為OC與AB的交點，E為線段OC延長線上一點，且∠EAC=∠ABC．
（1）求證：直線AE是⊙O的切線．
（2）若CD=6，AB=16，求⊙O的半徑；
（3）在（2）的基礎上，點F在⊙O上，且=?BC，△ACF的內心點G在AB邊上，求BG的長．?BF發布：2025/6/14 23:0:1組卷：1104引用：7難度：0.1