【數學概念】
有一條對角線平分一組對角的四邊形叫“對分四邊形”．
【概念理解】
（1）關于“對分四邊形”，下列說法正確的是 ①②①②．（填所有正確的序號）
①菱形是“對分四邊形”
②“對分四邊形”至少有兩組鄰邊相等
③“對分四邊形”的對角線互相平分
【問題解決】
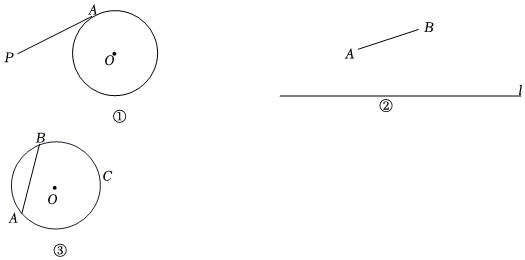
（2）如圖①，PA為⊙O的切線，A為切點．在⊙O上是否存在點B、C，使以P、A、B、C為頂點的四邊形是“對分四邊形”？
| 小明的作法： ①以P為圓心，PA長為半徑作弧，與⊙O交于點B； ②連接PO并延長，交⊙O于點C； ③點B、C即為所求． |
（3）如圖②，已知線段AB和直線l,請在圖②中利用無刻度的直尺和圓規，在直線l上作出點M、N，使以A、B、M、N為頂點的四邊形是“對分四邊形”．（只要作出一個即可，不寫作法，保留作圖痕跡）
（4）如圖③，⊙O的半徑為5，AB是⊙O的弦，AB=8，點C是⊙O上的動點，若存在四邊形ABCD是“對分四邊形”，且有一條邊所在的直線是⊙O的切線，直接寫出AC的長度．
【考點】圓的綜合題．
【答案】①②
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：971引用：3難度：0.1
相似題
-
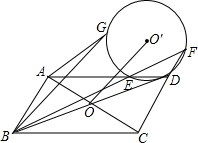1．如圖，已知四邊形ABCD是平行四邊形，AC，BD相交于O，∠ABC的平分線交CD的延長線于F，⊙O′是△DEF的外接圓，G是⊙O上一點，且AG=CD．求證：BG∥OO′．發布：2025/5/27 11:30:1組卷：82引用：1難度：0.5 -
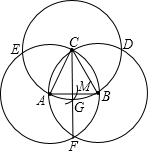2．如圖，分別以邊長1為的等邊三角形ABC的頂點為圓心，以其邊長為半徑作三個等圓，得交點D、E、F，連接CF交⊙C于點G，以點E為圓心，EG長為半徑畫弧，交邊AB于點M，求AM的長．發布：2025/5/27 4:30:2組卷：57引用：1難度：0.5 -
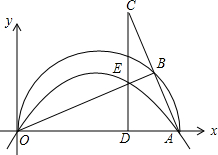3．如圖，在平面直角坐標系中，A（10，0），以OA為直徑在第一象限內作半圓，B為半圓上一點，連接AB并延長至C，使BC=AB，過C作CD⊥x軸于點D，交線段OB于點E．已知CD=8，拋物線經過O，E，A三點．
（1）求直線OB的函數表達式；
（2）求拋物線的函數表達式；
（3）若P為拋物線上位于第一象限內的一個動點，以P，O，A，E為頂點的四邊形面積記作S，則S取何值時，相應的點P有且只有3個．發布：2025/5/26 19:30:1組卷：111引用：1難度：0.3