請閱讀以下材料，并完成相應的任務．
| 【閱讀材料】 在《阿基米德全集》中的《引理集》中記述了偉大的古希臘數(shù)學家、哲學家、物理學家阿基米德提出的六個有關圓的引理，其中第二個引理是： 如圖1，點P是 ? AB ? AB ? PQ ? PA  |
（1）如圖2，小明同學嘗試說明“BQ=BD”，于是他連接了PA，PB，PD，PQ，請根據(jù)小明的思路完成后續(xù)證明過程；
（2）如圖3，以AB為直徑的半圓上有一點P，AP=6，AB=10，直線l與⊙O相切于點P，過點B作BE⊥l于點E，交⊙O于點Q，求出BQ的長．
【考點】圓的綜合題．
【答案】（1）見解析；
（2）．
（2）
14
5
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2024/8/25 18:0:8組卷：289引用：6難度：0.5
相似題
-
1．在⊙O中，直徑AB與弦CD（非直徑）交于點E，DE=CE，弦BG⊥BC交⊙O于點G，交CD于點F．
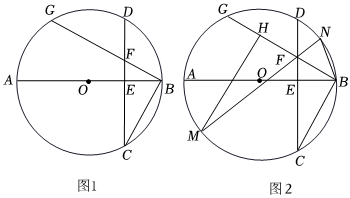
（1）如圖1，求證：∠ABF=∠BCD；
（2）如圖2，點N為弧BD上一點，連接BN、NF，并延長NF交⊙O于點M，H為FG上一點，連接MH，BN=BF，∠HMF=∠HBN，求證：FH=GH．12發(fā)布：2025/5/24 14:30:1組卷：107引用：1難度：0.1 -
2．已知在Rt△ABC中，∠C=90°，AC=
，BC=2．23
（1）如圖①，若P為BC上由點B向點C運動的一點，連接AP，設AP的中點為G，求在點P運動的過程中，點G經(jīng)過的路徑長．
（2）如圖②，若P是以AB為直徑所作半圓上由點A沿著半圓向點B運動的一點，求CP的中點F經(jīng)過的路徑長．
（3）如圖③，若P為BC上由點B向點C運動的一點，連接AP，作BR⊥AP于點R，（P、R可以重合）求在點P的運動過程中，R經(jīng)過的路徑長．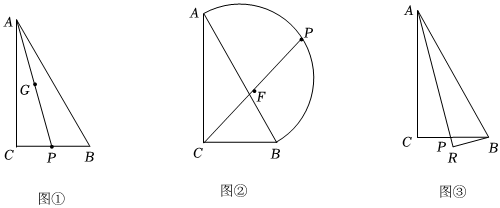
發(fā)布：2025/5/24 13:30:2組卷：86引用：1難度：0.3 -
3．如圖1，在Rt△ABC中，∠ABC=90°，以線段BC為直徑作⊙O交AC于點D，E為AB中點，連接ED，過點C作CF∥AB交ED的延長線于點F．
（1）求證：直線ED是⊙O的切線；
（2）判斷△CDF的形狀，并說明理由；
（3）如圖2，連接OF交⊙O于點P，連接BP交AC于點Q，若D為AQ中點，AB=6，求PQ的長．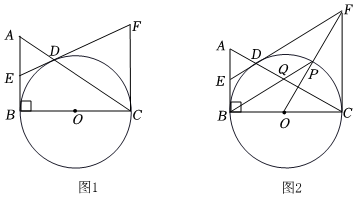
發(fā)布：2025/5/24 13:30:2組卷：319引用：2難度：0.3