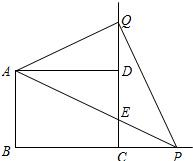
如圖，已知在矩形ABCD中，AB=3，BC=4，P是邊BC延長線上的一點，連接AP交邊CD于點E，把射線AP沿直線AD翻折，交射線CD于點Q，設CP=x,DQ=y.
（1）求y關于x的函數解析式，并寫出定義域；
（2）當點P運動時，△APQ的面積是否會發生變化？如果發生變化，請求出△APQ的面積S關于x的函數解析式，并寫出定義域；如果不發生變化，請說明理由；
（3）當以4為半徑的⊙Q與直線AP相切，且⊙A與⊙Q也相切時，求⊙A的半徑．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：489引用：11難度：0.3
相似題
-
1．如圖1，若△ABC內一點P滿足∠PAC=∠PBA=∠PCB，則點P為△ABC的布洛卡點，三角形的布洛卡點（Brocard point）是法國數學家和數學教育家克洛爾（A．L．Crelle1780-1855）于1816年首次發現，但他的發現并未被當時的人們所注意，1875年，布洛卡點被一個數學愛好者法國軍官布洛卡（ Brocard1845-1922）重新發現，并用他的名字命名．
問題：如圖2，在等腰△DEF中，DF=EF，FG是△DEF的中線，若點Q為△DEF的布洛卡點，FQ=9，=FGDE，則DQ+EQ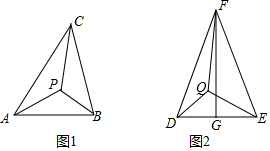=（ ）2
發布：2025/5/31 4:30:2組卷：917引用：3難度：0.6 -
2．如圖，正方形ABCD的邊長為2，E，F為線段AC上兩動點（不與A，C點重合），且∠EBF=45°．
（1）求證：△ABF∽△BEF．
（2）試說明無論點E，F在線段AC上怎樣運動，總有．（BEBF）2=CEAF發布：2025/5/31 1:30:2組卷：105引用：1難度：0.6 -
3．如圖，等邊三角形△ACB的邊長為3，點P為BC上的一點，點D為AC上的一點，連接AP、PD，∠APD=60°．
（1）求證：△ABP∽△PCD；
（2）若PC=2，求CD的長．發布：2025/5/31 1:30:2組卷：1863引用：18難度：0.6