如圖,在平面直角坐標系xOy中,正方形OABC的頂點B在第一象限,點A的坐標為(a,0).點P是正方形OABC四條邊上一動點(不與點O重合),將點P繞點O順時針旋轉45°得到點P′,稱點P′為正方形OABC的“伴隨點”.
(1)如圖1,若a=2,點P在邊BC上運動,
①當點P運動到點B時,正方形OABC的“伴隨點”P′的坐標為 (22,0)(22,0);
②當點P′恰好落在邊AB時,求此時點P′的坐標;
(2)如圖2,線段EF的端點坐標分別為E(3,2)、F(3,-1),若線段EF上存在正方形OABC的兩個“伴隨點”,求a的取值范圍;
(3)若正方形OABC的所有“伴隨點”中有6個整點(橫、縱坐標都是整數),直接寫出a的取值范圍.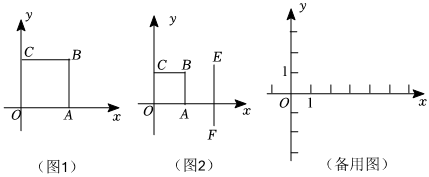
2
2
【考點】四邊形綜合題.
【答案】(2,0)
2
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/8/20 0:0:1組卷:52引用:1難度:0.2
相似題
-
1.已知△ABC是等邊三角形,四邊形ADEF是菱形,∠ADE=120°(AD>AB).
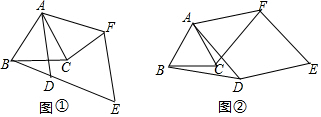
(1)如圖①,當AD與邊BC相交,點D與點F在直線AC的兩側時,BD與CF的數量關系為.
(2)將圖①中的菱形ADEF繞點A旋轉α(0°<α<180°),如圖②.
Ⅰ.判斷(1)中的結論是否仍然成立,請利用圖②證明你的結論.
Ⅱ.若AC=4,AD=6,當△ACE為直角三角形時,直接寫出CE的長度.發布:2025/6/25 7:30:2組卷:365引用:4難度:0.1 -
2.探究問題:
(1)方法感悟:
如圖①,在正方形ABCD中,點E,F分別為DC,BC邊上的點,且滿足∠EAF=45°,連接EF,求證DE+BF=EF.
感悟解題方法,并完成下列填空:
證明:延長CB到G,使BG=DE,連接AG,
∵四邊形ABCD為正方形,
∴AB=AD,∠ABC=∠D=90°,
∴∠ABG=∠D=90°,
∴△ADE≌△ABG.
∴AG=AE,∠1=∠2;
∵四邊形ABCD為正方形,
∴∠BAD=90°,
∵∠EAF=45°,
∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°.
∵∠1=∠2,
∴∠1+∠3=45°.
即∠GAF=∠.
又AG=AE,AF=AF,
∴△GAF≌.
∴FG=EF,
∵FG=FB+BG,
又BG=DE,
∴DE+BF=EF.
變化:在圖①中,過點A作AM⊥EF于點M,請直接寫出AM和AB的數量關系 ;
(2)方法遷移: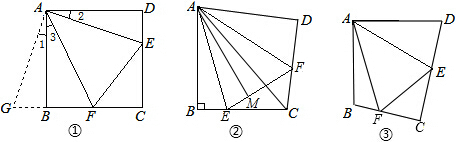
如圖②,將Rt△ABC沿斜邊AC翻折得到Rt△ADC,E,F分別是BC,CD邊上的點,∠EAF=∠BAD,連接EF,過點A作AM⊥EF于點M,試猜想DF,BE,EF之間有何數量關系,并證明你的猜想.試猜想AM與AB之間的數量關系,并證明你的猜想.12
(3)問題拓展:
如圖③,在四邊形ABCD中,AB=AD,E,F分別為DC,BC上的點,滿足∠EAF=∠DAB,試猜想當∠B與∠D滿足什么關系時,可使得DE+BF=EF.請直接寫出你的猜想(不必說明理由).猜想:∠B與∠D滿足關系:.12發布:2025/6/24 19:0:1組卷:881引用:1難度:0.1 -
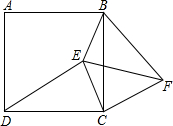 3.如圖,四邊形ABCD是正方形,E是正方形ABCD內一點,F是正方形ABCD外一點,連接BE、CE、DE、BF、CF、EF.
3.如圖,四邊形ABCD是正方形,E是正方形ABCD內一點,F是正方形ABCD外一點,連接BE、CE、DE、BF、CF、EF.
(1)若∠EDC=∠FBC,ED=FB,試判斷△ECF的形狀,并說明理由.
(2)在(1)的條件下,當BE:CE=1:2,∠BEC=135°時,求BE:BF的值.
(3)在(2)的條件下,若正方形ABCD的邊長為(3+3)cm,∠EDC=30°,求△BCF的面積.7發布:2025/6/24 17:30:1組卷:59引用:1難度:0.5


