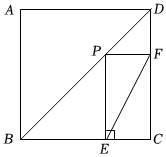
如圖，在邊長為2的正方形ABCD中，點M為對角線BD上一動點，ME⊥BC于點E，MF⊥CD于點F，連接EF，則EF的最小值為（ ）
【答案】D
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/6 8:0:9組卷：1068引用：4難度：0.6
相似題
-
1．正方形具有而菱形不具有的性質是（ ）
發布：2025/6/8 4:30:1組卷：278引用：11難度：0.9 -
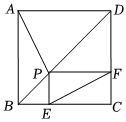2．如圖，已知正方形ABCD的邊長為4，P是對角線BD上一點，PE⊥BC于點E，PF⊥CD于點F，連接AP，EF，給出下列結論：①PD=EC；②AP=EF；③AP⊥EF；④EF的最小值為22；⑤△APD可能是等腰三角形．其中正確結論的序號為（ ）2發布：2025/6/8 5:0:1組卷：119引用：3難度：0.4 -
3．點E為正方形ABCD邊BC上的一點，點G為BC延長線一點，連接AE，過點E作AE⊥EF，且AE=EF，連接CF．
（1）如圖，求證：∠FCG=45°；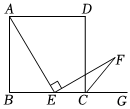
（2）如圖，過點D作DH∥EF交AB于點H，連接HE，求證：AH2+BH2=HE2；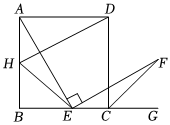
（3）如圖，連接AF、DF，若AF交CD于點M，DM=2，BH=3，求DF的長．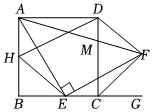
發布：2025/6/8 4:0:1組卷：137引用：1難度：0.2