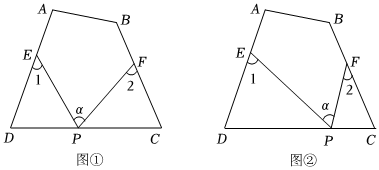
在四邊形ABCD中,∠A=100°,∠B=120°,點(diǎn)E、F分別是邊AD,BC上的點(diǎn),點(diǎn)P是一動(dòng)點(diǎn),令∠PED=∠1,∠PFC=∠2,∠EPF=∠α.
初探:
(1)如圖①,若點(diǎn)P在線段CD上,且∠α=70°,則∠1+∠2=110110°;
(2)如圖②,若點(diǎn)P在線段CD上運(yùn)動(dòng),試探究∠1+∠2與∠α之間的關(guān)系,并說明理由;
再探:
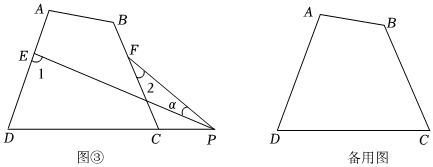
(3)如圖③,若點(diǎn)P在線段DC的延長線上運(yùn)動(dòng),則∠1,∠2,∠α之間的關(guān)系為 ∠1-∠2=∠a+40°或∠1+∠2+∠a=400°∠1-∠2=∠a+40°或∠1+∠2+∠a=400°;
(4)若點(diǎn)P運(yùn)動(dòng)到四邊形ABCD的內(nèi)部,直接寫出此時(shí)∠1,∠2,∠α之間的關(guān)系為 ∠1+∠2=∠a+40°∠1+∠2=∠a+40°.
【考點(diǎn)】多邊形內(nèi)角與外角.
【答案】110;∠1-∠2=∠a+40°或∠1+∠2+∠a=400°;∠1+∠2=∠a+40°
【解答】
【點(diǎn)評】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/6/27 10:35:59組卷:274引用:2難度:0.5







