問題情境：小明同學在八年級下冊數學書中遇到如下的一道題目：如圖1，在等邊△ABC中，點P是△ABC內一點，且PA=3，PB=5，PC=4，求∠APC的度數，
小明在解決這個問題是，想到了以下的思路，如圖2，把△APC繞著點A順時針旋轉，使點C旋轉到點B位置，得到△ADB，連接DP，
請你在小明思路的提示下，求出∠APC的度數；
方法應用：如圖3，點E是正方形ABCD內一點，連接AE，BE，DE，若AE=2，BE=26，∠AED=135°，求DE的長以及正方形ABCD的面積．
26
【考點】四邊形綜合題．
【答案】問題情境：150°；
方法應用：DE的長為3，正方形ABCD的面積為34．
方法應用：DE的長為3
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/12 20:0:2組卷：106引用：1難度：0.2
相似題
-
1．在正方形ABCD中，E是邊CD上一點（點E不與點C、D重合），連接BE．
【感知】如圖①，過點A作AF⊥BE交BC于點F．易證△ABF≌△BCE．（不需要證明）
【探究】如圖②，取BE的中點M，過點M作FG⊥BE交BC于點F，交AD于點G．
（1）求證：BE=FG．
（2）連接CM，若CM=1，則FG的長為 ．
【應用】如圖③，取BE的中點M，連接CM．過點C作CG⊥BE交AD于點G，連接EG、MG．若CM=3，則四邊形GMCE的面積為 ．發布：2025/6/13 19:30:1組卷：4524引用：23難度：0.1 -
2．已知，四邊形ABCD是矩形，AD＞AB，E、F、G分別是AB、BC、AD上的點，
，AEBE=n．ADBE=DEEF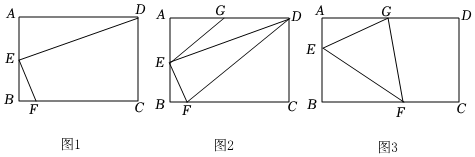
（1）當n=1，DE⊥EF．
①如圖1，求證：；ADBE=DEEF
②如圖2，連接DF，若CF=2AG，求；DFDG
（2）如圖3，，AD=2AB=10，∠GEF=45°，直接寫出△EFG面積的最小值．n=23發布：2025/6/13 17:30:5組卷：459引用：4難度：0.2 -
3．已知正方形ABCD與正方形AEFG，正方形AEFG繞點A旋轉一周．
（1）如圖①，連接BG、CF，求的值；CFBG
（2）當正方形AEFG旋轉至圖②位置時，連接CF、BE，分別取CF、BE的中點M、N，連接MN、試探究：MN與BE的關系，并說明理由；
（3）連接BE、BF，分別取BE、BF的中點N、Q，連接QN，AE=6，請直接寫出線段QN掃過的面積．
發布：2025/6/13 18:30:2組卷：3922引用：6難度：0.2