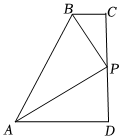
如圖，在四邊形ABCD中，P為CD邊上的一點，BC∥AD．AP、BP分別是∠BAD、∠ABC的角平分線．
（1）若∠BAD=70°，則∠ABP的度數為 55°55°，∠APB的度數為 90°90°；
（2）求證：AB=BC+AD；
（3）設BP=3a,AP=4a,過點P作一條直線，分別與AD，BC所在直線交于點E、F，若AB=EF，直接寫出AE的長（用含a的代數式表示）
【考點】四邊形綜合題．
【答案】55°；90°
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/30 4:0:3組卷：251引用：2難度：0.1
相似題
-
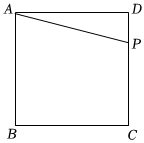1．如圖，正方形ABCD的邊長為4cm,P點從D出發以每秒鐘1cm的速度沿D→C→B→A的路線勻速運動（點P不與點D和點A重合），設點P運動的路程為x cm.
（1）求△APD的面積y cm2與x cm之間的函數關系式；
（2）畫出這個函數的圖象；
（3）根據圖象寫出函數值y隨自變量x的變化情況．發布：2025/6/4 5:30:2組卷：14引用：1難度：0.5 -
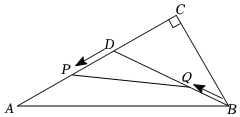2．如圖，在Rt△ABC中，∠A=30°，∠C=90°，AB=4cm,∠ABC的平分線BD交AC于點D．動點P從點D出發，沿DA方向勻速向點A運動，同時動點Q從點B出發，沿BD方向勻速向點D運動．已知點P、Q的運動速度都是1cm/s,當其中一個點到達終點時，另一個點也停止運動，設運動時間為t（s）（0＜t＜4），解答下列問題：3
（1）求BD長；
（2）在運動過程中，是否存在某一時刻t,使點D在線段PQ的垂直平分線上？若存在，求出t值；若不存在，請說明理由；
（3）當t=時，求四邊形PABQ的面積．52發布：2025/6/4 5:0:1組卷：290引用：4難度：0.4 -
3．閱讀下列材料：
利用完全平方公式，將多項式x2+bx+c變形為（x+k）2+h的形式，然后由（x+k）2≥0就可求出多項式x2+bx+c的最小值．
例題：求x2-14x+50的最小值．
解：x2-14x+50=x2-2x?7+72-72+50=（x-7）2+1．
因為不論x取何值，（x-7）2總是非負數，即（x-7）2≥0．所以（x-7）2+1≥1，
所以當x=7時，x2-14x+50有最小值，最小值是1．
根據上述材料，解答下列問題：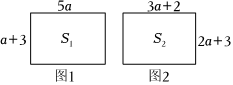
（1）填空：x2-16x+=（x-）2；
（2）將x2+32x-2變形為（x+k）2+h的形式，并求出x2+32x-2的最小值；
（3）如圖1所示的長方形邊長分別是5a、a+3，面積為S1；如圖2所示的長方形邊長分別是2a+3、3a+2，面積為S2，試比較S1與S2的大小，并說明理由．發布：2025/6/4 5:0:1組卷：95引用：2難度：0.3