問題初探：數學興趣小組在研究四邊形的旋轉時，遇到了這樣的一個問題．如圖1，四邊形ABCD和BEFG都是正方形，BH⊥AE于H，延長HB交CG于點M．通過測量發現CM=MG．為了證明他們的發現，小亮想到了這樣的證明方法：過點C作CN⊥BM于點N．他已經證明了△ABH≌△BCN，但接下來的證明過程，他有些迷茫了．
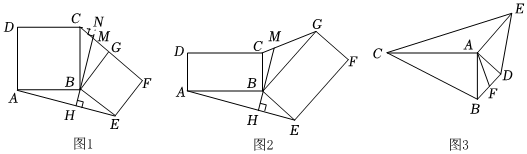
（1）請同學們幫小亮將剩余的證明過程補充完整；
（2）深入研究：若將原題中的“正方形”改為“矩形”（如圖2所示），且ABBC=BGBE=k（其中k＞0），請直接寫出線段CM、MG的數量關系為 MG=k2CMMG=k2CM；
（3）拓展應用：在圖3中，在Rt△ABC和Rt△ADE中，∠BAC=∠DAE=90°，∠ACB=∠AED=30°，連接BD、CE，F為BD中點，則AF與CE的數量關系為 CE=23AFCE=23AF．
AB
BC
=
BG
BE
=
k
CE
=
2
3
AF
CE
=
2
3
AF
【考點】相似形綜合題．
【答案】MG=k2CM；
CE
=
2
3
AF
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：220引用：2難度：0.3
相似題
-
1．在矩形ABCD中，AB=4，BC=3，E是AB邊上的一個動點（不與點A、B重合），EF⊥EC交AD于F，過點E作∠AEH=∠BEC，交射線AD于G，交射線CD于H．
（1）如圖1，當點G與點F重合時，求AE的長；
（2）如圖2，當點G在線段FD上時，設BE=x,DH=y,求y與x的函數關系式，并寫出自變量x的取值范圍；
（3）連接AC，以E、F、G為頂點的三角形能否與△AEC相似，如果能，請求出AE的長；如果不能，請說明理由．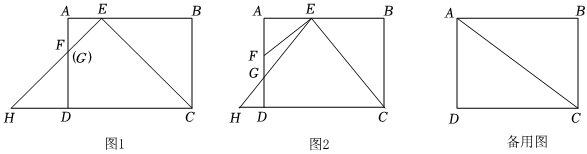
發布：2025/5/24 21:0:1組卷：61引用：1難度：0.1 -
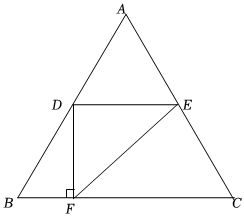2．如圖，等邊△ABC的邊長為4，點D在邊AB上運動，過點D作DF⊥BC于點F，過點D作DE∥BC，交AC于點E，連結EF，設DF=x,△DEF的面積為y.
（1）求y與x的函數關系式，并確定自變量x的取值范圍；
（2）當x為何值時，△DEF的面積有最大值？并求出最大值；
（3）當△DBF與由D、E、F三點組成的三角形相似時，求AD的長．發布：2025/5/24 21:30:1組卷：57引用：1難度：0.1 -
3．【基礎鞏固】
（1）如圖1，在△ABC中，D為AB上一點，∠ACD=∠B．求證：AC2=AD?AB．
【嘗試應用】
（2）如圖2，在平行四邊形ABCD中，E為BC上一點，F為CD延長線上一點，∠BFE=∠A．若BF=4，BE=3，求AD的長．
【拓展提高】
（3）如圖3，在菱形ABCD中，E是AB上一點，F是△ABC內一點，EF∥AC，AC=2EF，∠EDF=∠BAD，AE=2，DF=5，則菱形ABCD的邊長為 ．12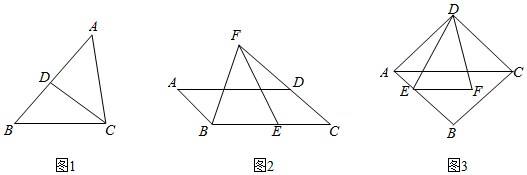
發布：2025/5/24 21:0:1組卷：2744引用：17難度：0.1