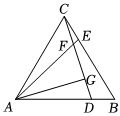
如圖，在等邊△ABC中，D、E分別為AB、BC邊上的兩動點，且總使AD=BE，AE與CD交于點F，AG⊥CD于點G．
（1）求證：△ACE≌△CBD；
（2）若EF=1，FG=3，求CD的長；
（3）連結DE，若DE⊥AB，已知BD=2，求等邊△ABC的邊長．

【答案】（1）見解答；
（2）7；
（3）2

．

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2025/5/24 0:0:1組卷：143引用：1難度：0.5

相似題

1．“三等分角”大約是在公元前五世紀由古希臘人提出來的，借助如圖所示的三等分角儀能三等分任一角，這個三等分角儀由兩根有槽的棒OA，OB組成，兩根棒在O點相連并可繞點O轉動，C點固定，OC=CD=DE，點D，E可在槽中滑動，若∠BDE=81°，則∠CDE的度數是（　　）
A．72° B．75° C．80° D．60°
發布：2025/5/25 18:30:1組卷：203引用：3難度：0.6
解析
2．正△ABC的邊長為4，D是AC的中點，P是△ABC內一點，且BP²+CP²=AP²，則PD的最小長度是
．
發布：2025/5/25 19:30:2組卷：474引用：1難度：0.2
解析
3．如圖，正方形ABCD中，P是對角線AC上的一個動點（不與A，C重合），連接BP，將BP繞點B順時針旋轉90°到BQ，連接QP交BC于點E，QP延長線與邊AD交于點F，連接CQ．則以下幾個結論：①AP=CQ；②∠APF=∠CBQ；③BE=BP；④PF=EQ．
所有正確結論的序號是（　　）
A．①② B．②④ C．①②③ D．①②④
發布：2025/5/25 22:30:2組卷：279引用：3難度：0.4
解析

相關試卷

如圖，在等邊△ABC中，D、E分別為AB、BC邊上的兩動點，且總使AD=BE，AE與CD交于點F，AG⊥CD于點G．（1）求證：△ACE≌△CBD；（2）若EF=1，FG=3，求CD的長；（3）連結DE，若DE⊥AB，已知BD=2，求等邊△ABC的邊長．