綜合與實踐
實踐情境：數學綜合與實踐課上，如圖①，老師發給每個小組一塊表面平整的矩形木板、一個內角為的直角三角板（說明：僅能作30°，60°，90°的角）和一把無刻度的直尺（說明：僅能作直線）、四只木工筆、小刀、橡皮、手工鋸子．
?
實踐任務：僅利用提供的工具將木板三等分，使原木板的寬作為等分后木板的一邊．對核心任務進行數學抽象：如圖②，已知矩形ABCD，利用含30°的直角三角板和無刻度直尺，在AB上確定點P，使BP=13AB．
下表是各小組展示完成實踐任務的操作步驟：
1
3
| 組別 | 操作步驟 | 圖示 |
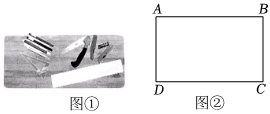
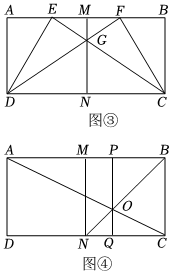
| A組 | 第一步：如圖③所示，分別以點D，點C為頂點，DA，CB為邊作30°的角與AB交于點E，F，連接DF，CE，交于點G，過點G作GM⊥A組AB于點M，并延長MG交CD于點N；第二步：如圖④所示，擦除線段DE，EC，DF，連接AC，BN交于點O，過點O作OP⊥AB于點P，并延長PO交CD于點Q． |
|
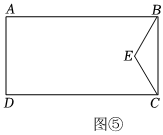
| B組 | 第一步：如圖⑤所示，分別以點C，點B為頂30°的角交于點E； 第二步：… |
|
（1）在圖③中，證明：點M為AB的中點；
（2）在圖④中，證明：
BP
=
1
3
AB
（3）B組某同學計劃先在BC上確定點F，使
BF
=
1
3
BC
BP
=
1
3
AB
【考點】四邊形綜合題．
【答案】（1）（2）證明見解析部分；
（3）作圖，理由見解析部分．
（3）作圖，理由見解析部分．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/22 8:0:8組卷：236引用：1難度：0.1
相似題
-
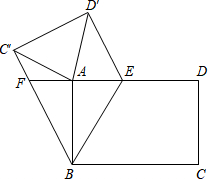1．如圖，在矩形ABCD中，AB=4，AD=6，E是AD邊上的一個動點，將四邊形BCDE沿直線BE折疊，得到四邊形BC′D′E，連接
AC′，AD′．
（1）若直線DA交BC′于點F，求證：EF=BF；
（2）當AE=時，求證：△AC′D′是等腰三角形；433
（3）在點E的運動過程中，求△AC′D′面積的最小值．發布：2025/5/24 17:0:2組卷：632引用：3難度：0.1 -
2．如圖，在平面直角坐標系中有矩形AOBC，AO=6，BO=8，連接OC，點P從頂點A出發以
個單位/秒的速度在線段AC上運動，同時點Q從頂點B出發以1個單位/秒的速度在線段BO上運動，只要有一個點先到達線段的另一個端點時，就停止運動．過點Q作QE⊥OB，交OC于點E，連接PE，設運動時間為t秒．32
（1）當t=2時，tan∠CPE=；
（2）當點P在線段AC．上運動時，設△PEC的面積為S，寫出S關于t的函數表達式，并寫出△PEC的面積最大時點E的坐標；
（3）直接寫出運動中，△PEC為等腰三角形時t的值．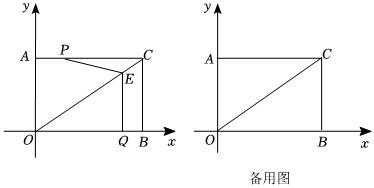
發布：2025/5/24 17:0:2組卷：26引用：1難度：0.1 -
3．如圖（1），已知矩形ABCD中，AB=6cm,BC=
cm,點E為對角線AC上的動點．連接BE．過E作EB的垂線交CD于點F．23
（1）探索BE與EF的數量關系，并說明理由．
（2）如圖（2），過F作AC的垂線交AC于點G，交EB于點H，連接CH．若點E從
A出發沿AC方向以cm/s的速度向終點C運動，設E的運動時間為t s.23
①是否存在t,使得H與B重合？若存在，求出t的值；若不存在，說明理由；
②t為何值時，△CFH是等腰三角形；
③當CG=GH時，求△CGH的面積．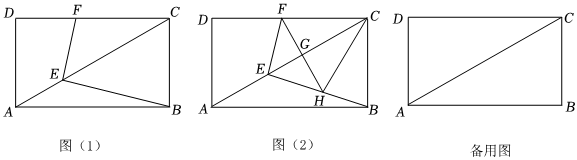
發布：2025/5/24 17:30:1組卷：221引用：1難度：0.2